
Alan Turing 1912-1954

Snapped for a passport photo

TuringA smile for his centenary
©B. Jack Copeland, Diane Proudfoot
Introduction
As anyone who can operate a personal computer knows, the way to make
the machine perform some desired task is to open the appropriate
program stored in the computer's memory. Life was not always so
simple. The earliest large-scale electronic digital computers, the
British Colossus (1944) and the American ENIAC (1945), did not store
programs in memory. To set up these
computers for a fresh task, it was necessary to modify some of the
machine's wiring, re-routing cables by hand and setting switches. The
basic principle of the modern computer—the idea of controlling
the machine's operations by means of a program of coded instructions
stored in the computer's memory—was conceived by Alan Turing.
Turing's abstract 'universal computing machine' of 1936, soon known
simply as the universal Turing machine, consists of a limitless
memory, in which both data and instructions are stored, and a scanner that moves back and forth through the memory, symbol by symbol,
reading what it finds and writing further symbols. By inserting different programs into the memory, the machine is made
to carry out different computations. It was a fabulous idea—a
single machine of fixed structure which, by making use of coded
instructions stored in memory, could change itself, chameleon-like,
from a machine dedicated to one task into a machine dedicated to a
quite different one.
Turing showed that his universal machine is able to accomplish any task that can be carried out by means of a rote method (hence the
characterization 'universal'). Nowadays, when so many people possess
a physical realization of the universal Turing machine, Turing's idea
of a one-stop-shop computing machine might seem as obvious as the
wheel. But in 1936, when engineers thought in terms of building
different machines for different purposes, Turing's concept was
revolutionary.
By the end of 1945, thanks to wartime developments in digital
electronics, groups in Britain and in the United States had embarked
on creating a universal Turing machine in hardware. Turing headed a
group situated at the National Physical Laboratory (NPL) in
Teddington, London. His technical report 'Proposed Electronic Calculator', dating
from the end of 1945 and containing his design for the Automatic
Computing Engine (ACE), was the first relatively complete
specification of an electronic stored-program digital computer.
In the United States the Hungarian-American mathematician John von
Neumann shared Turing's dream of building a universal stored-program
computing machine. Von Neumann had learned of the universal Turing
machine before the war—he and Turing came to know each other
during 1936-1938, when both were at Princeton University. Like
Turing, von Neumann became aware of the potential of high-speed
digital electronics as a result of wartime work. Von Neumann's 'First
Draft of a Report on the EDVAC', completed in the spring of 1945,
also set out a design for an electronic stored-program digital
computer ('EDVAC' stood for 'Electronic Discrete Variable Computer').
Von Neumann's report, to which Turing referred in 'Proposed
Electronic Calculator', was more abstract than Turing's, saying
little about programming or electronics. Harry Huskey, the electronic
engineer who subsequently drew up the first detailed hardware designs
for the EDVAC, said that the information in von Neumann's report was
of no help to him in this. Turing, in contrast, supplied detailed circuit designs, full
specifications of hardware units, specimen programs in machine code,
and even an estimate of the cost of building the ACE.
Part I of 'Alan Turing, Father of the Modern Computer' provides an
overview of Turing's many major contributions to the development of
the computer and computing—including his pioneering work in the
areas now called Artificial Intelligence and Artificial Life.
Part II tells the story of Turing's ACE. This
is simply one of the best tales in the history of computers. Right
from the start there was a mismatch of visions. Turing saw himself as
building 'a brain'. 'In working on the ACE', he said, 'I am more
interested in the possibility of producing models of the action of
the brain than in the practical applications to computing'. Turing's
employers, on the other hand, thought the ACE would be Britain's
national computer: a single machine that could satisfy the computing
needs of 'the whole country'. Frustration and disappointment dominate
the story. Woolly-minded administrators wasted the brilliant
technological achievements of Turing and his group. There is a happy
ending—but by that time Turing had turned his back on the ACE
forever. Much of Part II is in the words of the original
protagonists, drawn from documents of the time. (These and other
historic documents are now available online in The Turing Archive for
the History of Computing.)
Part III of 'Alan Turing, Father of the Modern Computer' is a digital
facsimile of 'Proposed Electronic Calculator', Turing's 48-page
report describing his revolutionary electronic computing machine.
Turing's original illustrations are included. (A paper version of the
report is available in the book Alan Turing's Automatic Computing Engine.)

The Mansion, Bletchley Park. Wartime headquarters of the Government Code and Cypher School.

The Bombe. Turing's Bombes turned Bletchley Park into a codebreaking factory.

The Pilot Model ACE
| 1936 |
The universal Turing machine |
| Turing leaves Cambridge for the Institute of Advanced Study at Princeton, where he continues his pioneering work in
recursion theory |
| 1938 |
Turing returns to Cambridge |
| 1939 |
At outbreak of war with Germany in September, Turing takes up residence at the Government Code and Cypher School, Bletchley Park |
| 1940 |
First Turing Bombe is installed at Bletchley Park |
| 1944 |
Colossus, the world's first large-scale electronic computer, is installed at Bletchley Park |
| 1945 |
Von Neumann's 'First Draft of a Report on the EDVAC' is circulated, setting out the design of the EDVAC (Electronic Discrete Variable Arithmetic Computer) |
| Turing joins the National Physical Laboratory |
| Turing's 'Proposed Electronic Calculator' is circulated, setting out the design of the ACE (Automatic Computing Engine) |
| Turing suggests (in 'Proposed Electronic Calculator') that computers will 'play very good chess' |
| ENIAC (Electronic Numerical Integrator and Computer) is the second large-scale electronic computer to operate |
| 1946 |
Turing and his group pioneer modern computer programming, writing a library of sophisticated programs for the unbuilt ACE |
| Turing presents a course of lectures on Versions V, VI, and VII of the ACE design, at the Ministry of Supply in London (Dec. 1946 to Feb. 1947). Kilburn attends from Manchester University |
| 1947 |
Turing lectures on the ACE at Burlington House in London, the first public lecture to mention computer intelligence |
| Darwin, Director of the National Physical Laboratory, halts work on ACE Test Assembly, leaving the field to Manchester |
| 1948 |
Manchester wins the race: the world's first stored-program electronic computer comes to life on June 21 in Newman's Computing Machine Laboratory |
| Turing, now at Manchester as Deputy Director of the Computing Machine Laboratory, writes 'Intelligent Machinery', the first manifesto of Artificial Intelligence |
| Turing's and Champernowne's 'Turochamp' plays its first game of chess |
| ENIAC is set up to run in (read-only) stored-program mode |
| 1949 |
Four more electronic stored-program computers become operational: EDSAC (Electronic Delay Storage Automatic Calculator) at the University of Cambridge, followed by BINAC (Binary Automatic Computer) in the U.S., the CSIR Mark I (Council for Scientific and Industrial Research Mark I Computer) in Australia, and Whirlwind I in the U.S. |
| Turing's paper 'Checking a Large Routine' inaugurates the area now known as 'program verification' |
| 1950 |
Pilot Model ACE is operational, preceded in the U.S. by SEAC (National Bureau of Standards Eastern Automatic Computer) and
followed by SWAC (National Bureau of Standards Western Automatic
Computer) |
| Turing publishes 'Computing Machinery and Intelligence', proposing the 'imitation game' or Turing Test |
| 1951 |
The Ferranti Mark I is the first commercially-available electronic stored-program computer. The first off the production line is installed at Manchester University |
| Turing begins using the Ferranti Mark I to study biological growth |
| UNIVAC is the first commercially-available electronic stored-program computer in the U.S. |
| von Neumann's computer at the Princeton Institute for Advanced Study is operational |
| Oettinger at Cambridge University writes the first program capable of learning |
| 1952 |
EDVAC is operational in the US |
| Strachey's draughts (checkers) program plays its first game on the Manchester computer |
| 1953 |
Turing publishes his classic paper on computer chess |
| 1954 |
Turing dies at his home in mysterious circumstances, age 41 |
| The world's first single-user desk-side computer, the G15, is operational in California |
| 1955 |
First DEUCE, production version of the Pilot Model ACE, is installed at the National Physical Laboratory |
| 1956 |
Dartmouth Summer Research Project on Artificial Intelligence |
| 1958 |
Big ACE operational at the National Physical Laboratory |

Turing
1. The Universal Turing Machine

King's College, Cambridge. Here Turing wrote ‘On Computable Numbers’. Photo © Andrew Pearce,
Fotogenix.co.uk
Turing introduced
his abstract Turing machines in his first major publication, 'On Computable Numbers, with an
Application to the Entscheidungsproblem' (1936). (Turing referred to these simply as 'computing machines'—the
American logician Alonzo Church dubbed them 'Turing machines'.)
'On Computable Numbers' pioneered the idea essential to the modern
computer—the concept of controlling a computing machine's
operations by means of a program of coded instructions stored in the
machine's memory. This work had a profound influence on the
development in the 1940s of the electronic stored-program digital
computer, an influence often neglected or denied by historians
of the computer.
A Turing machine is an abstract conceptual model. It consists of a
scanner and a limitless memory-tape. The tape is divided into
squares, each of which may be blank or may bear a single symbol ('0'
or '1', for example, or some other symbol taken from a finite
alphabet). The scanner moves back and forth through the memory,
examining one square at a time (the 'scanned square'). It reads the
symbols on the tape and writes further symbols. The tape is both the
memory and the vehicle for input and output. The tape may also
contain a program of instructions. The tape itself is
limitless—in fact Turing's aim was to show that there are tasks
that Turing machines cannot perform, even given unlimited working
memory and unlimited time.
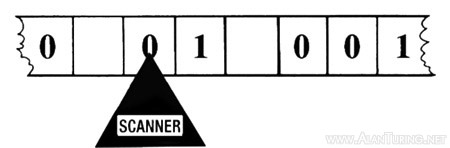
The scanner and tape
A Turing machine has a small repertoire of basic operations: move
left one square, move right one square, print, and change state. Movement is always by one square at a time. The
scanner can print a symbol on the scanned square (after erasing any
existing symbol). By changing its state the machine can, as Turing
put it, 'remember some of the symbols which it has "seen"
(scanned) previously'. Turing did not specify a mechanism for changing state—Turing
machines are abstractions and proposing a specific mechanism is
unnecessary—but one can easily be imagined. Suppose that a device
within the scanner consists of a dial with a finite number of
positions, labelled 'a', 'b', 'c', and so on, each position counting
as a different state. Changing state consists in shifting the dial's
pointer from one labelled position to another. This device functions
as a simple memory; for example, a dial with three positions can be
used to record whether the square that the scanner has just vacated
contained '0' or '1', or was blank.
STATE |
SCANNED
SQUARE |
OPERATIONS |
NEXT
STATE |
a |
blank |
P[0],
R |
b |
b |
blank |
R |
c |
c |
blank |
P[1],
R |
d |
d |
blank |
R |
a |
An instruction table or ‘program’ for a Turing machine
The operation of the machine is governed by (what Turing called) a
table of instructions. He gave the following simple example. A machine—call it M—begins work with an endless
blank tape and with the scanner positioned over any square of the
tape. M has four states, labelled 'a', 'b', 'c',
and 'd', and is in state a when it starts work. In the
table shown, 'R' is an abbreviation of the instruction 'move right
one square', 'P[0]' is an abbreviation of 'print 0 on the scanned
square', and analogously 'P[1]'. The top line of the table reads: if
you are in state a and the square you are scanning is blank,
then print 0 on the scanned square, move right one square, and go
into state b.
Acting in accordance with this table of instructions—or
program—M prints alternating binary digits on the tape, 0 1 0 1
0 1..., working endlessly to the right from its starting place,
leaving a blank square in between each digit.
The UTM

The
Essential Turing (Oxford University Press, 2004, ed. Copeland) gives a full account of how Turing machines work, and also of the Bletchley Park codebreaking operation and Turing's work on Enigma, including Turing's own description of the Bombe.
The UTM (universal Turing machine) is universal in the sense that it
can be programmed to carry out any calculation that could in
principle be performed by a 'human computer'—a clerk who works
in accordance with an 'effective' or rote procedure. Before the advent of the electronic computer, many thousands
of human computers were employed in business, government, and
research establishments. The universal machine has a single, fixed
table of instructions built into it—'hard-wired', so to speak, into
the machine. Operating in accordance with this one fixed table, the
UTM can read and execute coded instructions inscribed on its tape.
This is the 'stored program' concept, the idea of controlling the
function of the computing machine by storing a program of
instructions in the machine's memory.
An instruction table for carrying out a desired task is placed on the
UTM's tape in a suitably encoded form, the first line of the table
occupying the first so many squares of the tape, the second line the
next so many squares, and so on. (Turing referred to this encoded form
of the instructions as the 'standard description' of the instruction
table.) The UTM reads the instructions and carries them out on its
tape. Different programs can be inscribed on the tape, enabling the
UTM to carry out any task for which a Turing-machine instruction
table can be written—thus a single machine of fixed structure is able to carry out every computation that can
be carried out by any Turing machine whatsoever.
In 1936 the UTM existed only as an idea. But right from the start
Turing was interested in the possibility of actually building such a
machine. His wartime acquaintance with electronics was the key link between
his earlier theoretical work and his 1945 design for an electronic
stored-program digital computer.
2. Codebreaking in World War II

Enigma machine with its wheels, lamps and plugboard exposed. Once the operator has inserted the correct wheels for the day he closes the inner lid.

Thomas H. Flowers, creator of Colossus

The Lorenz Schlüsselzusatz (cipher attachment) was code-named 'Tunny' by the British

Colossus and two operators, Dorothy Du Boisson (left) and Elsie Booker

Robinson, precursor to Colossus. This machine, which eventually came to be known as 'Old Robinson', replaced the original 'Heath Robinson' (the two were similar in appearance).

Turing completed the logical design of the famous Bombe—built
to break German Enigma messages—in the last months of 1939.His
designs were handed over to Harold 'Doc' Keen at the British Tabulating Machine
Company in Letchworth, where the engineering development was carried
out. The first bombe, named 'Victory', was installed at the Government
Code and Cypher School (GC & CS) at Bletchley Park early in 1940
and an improved model 'Agnus Dei' (later
corrupted to 'Agnes' and 'Aggie') was installed in the summer of that
year. Agnus contained Gordon Welchman's ingenious 'diagonal board'.
The Bombe was a 'computing machine'—a term for any machine able
to do work that could in principle be done by a human computer—but one with a
very narrow and specialized purpose, namely searching through the
wheel-positions of the Enigma machine, at superhuman speed, in order
to find the positions at which a German message had been encrypted.
The Bombe produced likely candidates, which were tested by hand on an
Enigma machine (or a replica of one)—if German text emerged (even a
few words followed by nonsense), the candidate settings were the
right ones.
The Bombe was based on the electromagnetic relay, although some later
versions were electronic (i.e. based on valves or vacuum tubes) and in consequence
faster. Relays are small switches consisting of a moving metal rod
which opens and closes an electrical circuit; the rod is moved by
means of a magnetic field. Electronic valves (called 'vacuum tubes'
in the U.S.) operate very many times faster than relays, since the
valve's only moving part is a beam of electrons.
During the attack on Enigma, Bletchley Park approached the Post
Office Research Station at Dollis Hill in London to build a
relay-based machine for use in conjunction with the Bombe. Once the
Bombe had uncovered the Enigma settings used to encrypt a particular
message, these settings were to be transferred to the proposed
machine, which would then automatically decipher the message and
print out the original German text. Dollis Hill sent engineer Thomas Flowers to Bletchley
Park. In the end, the machine Flowers built was not used, but he was
soon to become one of the great figures of World War II codebreaking.
Thanks to his pre-war research, Flowers was (as he himself remarked)
possibly the only person in Britain who realized that valves could be
used on a large scale for high-speed digital computing.
The world's first large-scale electronic digital computer, Colossus,
was designed and built during 1943 by Flowers and his team at Dollis
Hill, in consultation with the Cambridge mathematician Max Newman,
head of the section at Bletchley Park known simply as the 'Newmanry'. (Turing had attended Newman's lectures on mathematical logic at
Cambridge before the war; these lectures launched Turing on the
research that led to his 'On Computable Numbers'.)
Colossus was operational at the beginning of 1944, two years before the first comparable U.S. machine, the ENIAC, was working.
It was used against the Lorenz cipher machine, more advanced
than Enigma and introduced in 1941.
Turing had briefly joined the attack on the Lorenz machine in 1942,
devising a cryptanalytical method known simply as 'Turingery'.
Turingery was the third of the three strokes of genius that Turing
contributed to the attack on the German codes—the others being his design
for the Bombe and unravelling of the form of Enigma used by the
Atlantic U-boats (see The Essential Turing). As fellow codebreaker Jack Good observed, 'I
won't say that what Turing did made us win the war, but I daresay we
might have lost it without him'.
Turingery was a hand method, involving paper, pencil and eraser.
Basic to Turingery was the idea of forming what was called the
'delta' of a stream of letters. The delta of a letter-stream is the
stream that results from adding together each pair of adjacent
letters (Turingery and delta-ing are both explained in detail in Colossus: The Secrets of Bletchley Park's Codebreaking Computers).
Turing discovered that delta-ing would reveal information that
was otherwise hidden. His discovery was essential to the developments
that followed: the algorithms implemented in Colossus (and in its
precursor Heath Robinson) depended on this simple but brilliant
observation. In that sense, the entire machine-based attack on the Lorenz machine
flowed from this fundamental insight of Turing's.
The British government kept Colossus secret: before the 1970s few had
any idea that electronic computation had been used successfully
during World War II, and it was not until 2000 that the British and
the U.S. finally declassified the complete account of Colossus'
wartime role. So it was that, in the decades following the war, von Neumann and
others told the world that the ENIAC was 'the first electronic
computing machine'. (In fact, what was arguably the first small-scale electronic computer
was put together at Iowa State College by John Atanasoff and his
student Clifford Berry. Their tiny digital computer contained approximately 300 valves,
compared to Colossus's 2400. Designed for one very specific
mathematical task (solving systems of linear algebraic equations),
Atanasoff's machine had virtually no programmability. Although its
electronic circuits functioned, the computer as a whole never worked
properly, because errors were introduced by an unsatisfactory binary
card-reader. The computer was left unfinished in 1942 when Atanasoff
moved away from Iowa State College.)
Flowers had established decisively and for the first time that
large-scale electronic computing machinery was practicable. However,
while Colossus possessed a considerable amount of flexibility, it was
far from universal. Nor did it store instructions internally. As with
the later ENIAC, in order to set Colossus up for a new job it was
necessary to modify some of the machine's wiring manually, by means
of plugs and switches. During the construction of Colossus, Newman
showed Flowers Turing's 'On Computable Numbers', with the key idea of
storing coded instructions in memory, but Flowers did not follow it
up.
Flowers has said that, once Turing saw Colossus in operation, it was
just a matter of Turing's waiting to see what opportunity might arise
to put the idea of his universal computing machine into practice. There is little doubt that by 1944 Newman too had firmly in mind the
possibility of building a universal machine using electronic
technology. In February 1946, a few months after his
appointment as Professor of Mathematics at the University of
Manchester, Newman wrote to von Neumann in the U.S.:
I am ...
hoping to embark on a computing machine section here, having got very
interested in electronic devices of this kind during the last two or
three years. By about eighteen months ago I had decided to try my
hand at starting up a machine unit when I got out... . I am of course in close touch with Turing.
Newman's story is continued in chapter 11 The Manchester Computer.
Turing's own opportunity came when John Womersley appeared out of
the blue: see
chapter 15 Womersley Recruits Turing to the National Physical
Laboratory. By
then Turing had taken pains to educate himself in electronic
engineering (during the later part of the war he himself gave a
series of evening lectures 'on valve theory').
3. Turing's Design for the Automatic Computing Engine (ACE)

Bushy House, part of the National Physical Laboratory. The Pilot Model of the Automatic Computing Engine was built here in what was originally the butler's pantry.
Turing saw that speed and memory were the keys to computing (in the
words of his assistant at the NPL, Jim Wilkinson, Turing was
'obsessed with the idea of speed on the machine').
Turing's design for the ACE had much in common with today's RISC
(Reduced Instruction Set Computer) architectures and called for a
high-speed memory of roughly the same capacity as an early Apple
Macintosh computer and enormous by the standards of his day.
Turing's ACE and the EDVAC—which was not completed until 1952—
differed fundamentally in design.
The EDVAC had (what is now called) a central processing unit or cpu,
whereas in the ACE the different temporary stores and other memory
locations had specific logical or numerical functions, e.g. addition, associated with
them. For example, if two numbers were transferred to a certain
named destination in memory, their sum would be formed there (ready to be
transferred elsewhere by a subsequent instruction). Unlike the EDVAC with its cpu, in the ACE there was no single place where all the logical and numerical operations were done.
The ACE's programs were made up entirely of instructions like
'Transfer the contents of Temporary Store 15 to Temporary Store 16'. Instead of writing
mathematically significant instructions such as
ADD x to y AND STORE THE RESULT IN z
or
MULTIPLY x BY y AND STORE THE RESULT IN z
someone programming the ACE had to compose a series of 'low-level' transfer instructions
producing the same effect. A related difference between the ACE and the EDVAC was that, in Turing's
design, complex behaviour was to be achieved by complex programming
rather than by complex equipment. Turing's philosophy was to dispense with
additional hardware (such as a multiplier, divider, and hardware for
floating-point arithmetic) in favour of software, and he spoke
disparagingly of 'the American tradition of
solving one's difficulties by means of much equipment rather than
thought'.

In order to increase the speed of a program's execution, Turing
proposed that instructions be stored, not consecutively in memory, but at
carefully chosen positions, with each instruction
containing a reference to the position of the next. This meant that each instruction was available at exactly the moment it was required, with no delays. Also with a view
to speed, he included a small fast-access memory for the temporary
storage of whichever numbers were most frequently used at a given
stage of a computation. According to Wilkinson in 1955, Turing was
'the first to realise that it was possible to overcome access time
difficulties with ... mercury lines ... or drum stores by providing a
comparatively small amount of fast access store. Many of the
commercial machines in the USA and ... in this country make great use
of this principle.'
Administrative delays at the NPL (described in Part II) meant that it was
several years after the completion in 1945 of Turing's design paper
'Proposed Electronic Calculator' before any significant
progress was made on the physical construction of the ACE. While
waiting for the hardware to be built, Turing and his group pioneered
the science of computer programming, writing a library of
sophisticated mathematical programs for the planned machine (see
chapter 17 Turing Pioneers Computer Programming). Early in 1947 members of Turing's
group began to construct a minimal version of the ACE called the Test
Assembly (see chapter 19 Second Attempt to Build the ACE: the Huskey
Era and the Test Assembly). Unfortunately, work on this small computer was
stopped later that year by the NPL's inept management. Had the
project continued, the Test Assembly would probably have become the
world's first functioning electronic stored-program computer—an
honour that in the event went to the Manchester 'Baby', itself a very limited machine (see chapter 11 The Manchester
Computer).
4. The ACE as Descendant of the Universal Turing Machine

Turing

King's College, Cambridge, birthplace of the universal Turing machine and the stored program concept. Photo © Andrew Pearce,
Fotogenix.co.uk
Notoriously, Turing's universal machine of 1936 received no explicit
mention in 'Proposed Electronic Calculator' and some have questioned
whether the universal machine was an
ancestor of the ACE at all. However, some fragmentary notes by Turing
cast light on this issue. The notes are pages from a draft of
'Proposed Electronic Calculator', and in them Turing related the ACE
to the universal Turing machine. He explained why the memory
arrangement described in 'On Computable Numbers' could not 'be taken
over as it stood to give a practical form of machine'. (The notes are in Alan Turing's Automatic Computing
Engine.)
In a lecture given in 1947 Turing made it clear that he regarded the
ACE as a 'practical version' of the universal Turing machine:
Some years ago I was researching on what might
now be described as an investigation of the theoretical possibilities
and limitations of digital computing machines. I considered a type of
machine which had a central mechanism, and an infinite memory which
was contained on an infinite tape ...
It can be shown that a single special machine of that type can be
made to do the work of all... . The special machine may be called the universal machine; it works in
the following quite simple manner. When we have decided what machine
we wish to imitate we punch a description of it on the tape of the
universal machine... . The
universal machine has only to keep looking at this description in
order to find out what it should do at each stage. Thus the
complexity of the machine to be imitated is concentrated in the tape
and does not appear in the universal machine proper in any way... . [D]igital computing machines such as the ACE ...
are in fact practical versions of the universal machine. There is a
certain central pool of electronic equipment, and a large memory.
When any particular problem has to be handled the appropriate
instructions for the computing process involved are stored in the
memory of the ACE ...
A letter from Turing to the cyberneticist W. Ross Ashby again
highlights the fundamental point of similarity between the ACE and
the universal Turing machine:
The ACE is in fact, analogous to the 'universal
machine' described in my paper on conputable [sic] numbers ...
[W]ithout altering the design of the machine itself, it can, in
theory at any rate, be used as a model of any other machine, by
making it remember a suitable set of instructions.
5. The ACE and the American EDVAC

Kite Sharpless and the EDVAC (Philadelphia Evening Bulletin, 3 March 1947)

John von Neumann
In the years immediately following the Second World War John von Neumann
made the concept of the stored-program digital computer widely known,
through his writings and charismatic public addresses. Von Neumann
wrote 'First Draft of a Report on the EDVAC' and subsequently
directed the computer project at the Princeton Institute of Advanced
Study. The ensuing machine, the IAS computer, although not the first
to run in the U.S. (it began work in the summer of 1951),
was the most influential of the early U.S. computers and the
precursor to the IBM 701, the company's first mass-produced
stored-program electronic computer.
Von Neumann's 'First Draft of a Report on the EDVAC' was widely
read. Turing certainly expected readers of his 'Proposed Electronic
Calculator' to be familiar with the 'First Draft'. At the end of the
first section of 'Proposed Electronic Calculator' he said:
The present report gives a fairly complete
account of the proposed calculator. It is recommended however that it
be read in conjunction with J. von Neumann's '[First Draft of a]
Report on the EDVAC'.
To what extent was the content of 'Proposed Electronic Calculator'
influenced by the 'First Draft' (which preceded it by a few months)?
Turing's paper follows von Neumann's terminology and notation to some
extent—a sensible decision, making
it more likely that Turing's report would be readily understood. In
order to depict the EDVAC's logic gates, von Neumann had used a
modified version of a diagrammatic notation introduced by McCulloch and Pitts in connection with neural nets. Turing adopted this modified notation and in fact considerably extended it. There is no doubt that Turing simply borrowed some of the more
elementary material from the 'First Draft'. For example, his diagram
of an adder (figure 10 of 'Proposed Electronic Calculator') is essentially
the same as von Neumann's figure 3. A newspaper report in 1946 said that Turing 'gives credit for the
donkey work on the A.C.E. to Americans'.
However, Turing's logic diagrams provide detailed designs for
the logical control and the arithmetic part of the calculator and go
far beyond anything to be found in the 'First Draft'. The
similarities between 'Proposed Electronic Calculator' and the 'First
Draft' are relatively minor in comparison to the striking differences
in the designs that they contain. Moreover, von Neumann's minor
influence on 'Proposed Electronic Calculator' should not be allowed
to mask the extent to which Turing's universal machine of 1936 was
itself a fundamental influence upon von Neumann.

von Neumann beside the IAS computer at Princeton. The row of cannisters is the high-speed memory. Each cannister contains a single cathode ray tube known as a 'Williams tube' after its inventor, F. C. Williams.

The ENIAC. Although standardly described as the 'first electronic computer', the ENIAC in fact went into operation two years later than Colossus.
6. Turing's Influence on EDVAC Pioneer John von Neumann
In the secondary literature, von Neumann is often said to have
invented the stored-program computer, but he repeatedly emphasized
that the fundamental conception was Turing's. Von Neumann became
familiar with ideas in 'On Computable Numbers' during Turing's time
at Princeton (1936-38). He was soon intrigued by Turing's
concept of a universal computing machine. It was von Neumann who placed Turing's concept into the hands of
American engineers. Stanley Frankel (the Los Alamos physicist
responsible, with von Neumann and others, for mechanizing the
large-scale calculations involved in the design of the atomic and
hydrogen bombs) recorded von Neumann's view of the importance of 'On
Computable Numbers':
I know that in or about 1943 or '44 von Neumann
was well aware of the fundamental importance of Turing's paper of
1936 'On computable numbers ...',
which describes in principle the 'Universal Computer' of which every
modern computer (perhaps not ENIAC as first completed but certainly
all later ones) is a realization. Von Neumann introduced me to that
paper and at his urging I studied it with care. Many people have
acclaimed von Neumann as the 'father of the computer' (in a modern
sense of the term) but I am sure that he would never have made that
mistake himself. He might well be called the midwife, perhaps, but he
firmly emphasized to me, and to others I am sure, that the
fundamental conception is owing to Turing - insofar as not
anticipated by Babbage, Lovelace, and others. In my view von
Neumann's essential role was in making the world aware of these
fundamental concepts introduced by Turing and of the development work
carried out in the Moore school and elsewhere.
In 1944, von Neumann joined the Eckert-Mauchly ENIAC group at the
Moore School of Electrical Engineering at the University of
Pennsylvania. (At that time he was involved in the Manhattan Project
at Los Alamos, where roomfuls of clerks armed with desk calculating
machines were struggling to carry out the massive calculations
required by the physicists.) ENIAC—which had been under
construction since 1943—was, as mentioned above, not a
stored-program computer; instead programming consisted of re-routing cables
and setting switches. Moreover, the ENIAC was far from universal, having been
designed with only one very specific task in mind, the calculation of
trajectories of artillery shells.

Turing's 1947 sketch of a mercury delay line

Type of mercury delay line known as a 'trombone'

The Princeton Institute for Advanced Study, home of von Neumann's computer project. Photo © Thomas Uphill.

Turing

von Neumann

von Neumann
Von Neumann brought his knowledge of 'On Computable Numbers' to the
practical arena of the Moore School. Thanks to Turing's abstract
logical work, von Neumann knew that, by making use of coded
instructions stored in memory, a single machine of fixed structure
can in principle carry out any task for which a program can be
written. When ENIAC engineer Presper Eckert described his idea of
using the mercury delay line as a high-speed recirculating memory,
von Neumann saw that this was the means to make concrete the abstract
universal computing machine of 'On Computable Numbers'. (Turing explains mercury delay line memory on pages 4-5 of Part III.)
When, in 1946, von Neumann established his own project to build a
stored-program computer at the Institute for Advanced Study, he gave
his engineers 'On Computable Numbers' to read. Julian Bigelow, von Neumann's chief engineer and largely responsible
for the engineering design of the computer built at the Institute,
said:
The person who really ...
pushed the whole field ahead was von Neumann, because he understood
logically what [the stored-program concept] meant in a deeper way
than anybody else... . The
reason he understood it is because, among other things, he understood
a good deal of the mathematical logic which was implied by the idea,
due to the work of A. M. Turing ...
in 1936-1937 ... . Turing's [universal] machine does not sound much like a modern
computer today, but nevertheless it was. It was the germinal idea.
... So ...
[von Neumann] saw ... that
[the ENIAC] was just the first step, and that great improvement would
come.
Von Neumann repeatedly emphasized the fundamental importance of 'On
Computable Numbers' in lectures and in correspondence. In 1946 he
wrote to the mathematician Norbert Wiener of 'the great positive
contribution of Turing'—Turing's mathematical demonstration
that 'one, definite mechanism can be "universal"'. In 1948, in a lecture entitled 'The General and Logical Theory of
Automata', von Neumann said:
The English logician, Turing, about twelve years
ago attacked the following problem. He wanted to give a general
definition of what is meant by a computing automaton... . Turing carried out a careful analysis of what mathematical processes
can be effected by automata of this type... . He ... also introduce[d]
and analyse[d] the concept of a 'universal automaton' ...
An automaton is 'universal' if any sequence that can be produced by
any automaton at all can also be solved by this particular automaton.
It will, of course, require in general a different instruction for
this purpose. The Main Result of the Turing Theory. We might
expect a priori that this is impossible. How can there be an
automaton which is at least as effective as any conceivable
automaton, including, for example, one of twice its size and
complexity? Turing, nevertheless, proved that this is possible.
The following year, in a lecture delivered at the University of
Illinois entitled 'Rigorous Theories of Control and Information',
von Neumann said:
The importance of Turing's research is just
this: that if you construct an automaton right, then any additional
requirements about the automaton can be handled by sufficiently
elaborate instructions. This is only true if [the automaton] is
sufficiently complicated, if it has reached a certain minimal level
of complexity. In other words ...
there is a very definite finite point where an automaton of this
complexity can, when given suitable instructions, do anything that
can be done by automata at all.
Many books on the history of computing in the U.S. make no mention of
Turing. No doubt this is in part explained by the absence of any
explicit reference to Turing's work in the series of technical
reports in which von Neumann, with various co-authors, set out a
logical design for an electronic stored-program digital computer. Nevertheless there is evidence in these documents of von Neumann's
knowledge of Turing's 'On Computable Numbers'. For example, in the
report entitled 'Preliminary Discussion of the Logical Design of an
Electronic Computing Instrument' (1946), von Neumann and his
co-authors, Arthur Burks and Herman Goldstine (former
members of the ENIAC group who had joined von Neumann at the
Institute for Advanced Study) wrote the following:
First Remarks on the Control and Code:
It
is easy to see by formal-logical methods, that there exist codes that
are in abstracto adequate to control and cause the execution of any
sequence of operations which are individually available in the
machine and which are, in their entirety, conceivable by the problem
planner. The really decisive considerations from the present point of
view, in selecting a code, are more of a practical nature: Simplicity
of the equipment demanded by the code, and the clarity of its
application to the actually important problems together with the
speed of its handling of those problems.
Burks has confirmed that the first sentence of this passage is a
reference to the universal Turing machine. (The report was not intended for formal publication and no attempt
was made to indicate those places where reference was being made to
the work of others.)
The passage just quoted is in fact an excellent summary of the situation at
that time. In 'On Computable Numbers' Turing had shown in abstracto
that, by means of instructions expressed in the programming code of
his 'standard descriptions', a single machine of fixed structure is
able to carry out any task that a 'problem planner' is able to
analyse into effective steps. By 1945, considerations in abstracto
had given way to the practical problem of devising an equivalent
programming code that could be implemented efficiently by means of
electronic circuits. Von Neumann's embryonic code appeared in the
'First Draft'. 'Proposed Electronic Calculator' set out Turing's own
very different and much more fully-developed code.
7. The Pilot Model ACE and the Production Model DEUCE

The Pilot Model of Turing's Automatic Computing Engine. The Pilot ACE was the fastest of the early electronic computers.

The NPL DEUCE in 1958

Advertisement for the Bendix G15, a desk-side computer based on Turing's ACE design

Three of MOSAIC's racks. A large computer built to Turing's design, the MOSAIC was used for secret work during the Cold War.
Had Turing's ACE been built as planned, it would have been in a
different league from the other early computers, but his colleagues
at the NPL thought the engineering work too ambitious and a
considerably smaller machine was built. Known as the Pilot Model ACE,
this machine ran its first program on 10 May 1950. With
a clock speed of 1 MHz it was for some time the fastest computer in
the world. Despite having only a few per cent of the memory capacity
that Turing had specified, the Pilot ACE in other respects adhered
closely to what Turing called 'Version V' of his ACE design.
The English Electric Company built a production version of the Pilot
Model ACE called the 'DEUCE' (Digital Electronic Universal Computing
Engine). The first DEUCE was delivered
in March 1955 (to the NPL). The DEUCE was a huge success and more
than 30 were sold—confounding the suggestion made in 1946 by
the Director of the NPL, Sir Charles Darwin, that 'it is very
possible that ... one machine would suffice to solve all the problems
that are demanded of it from the whole country'. DEUCEs were used for many scientific, industrial and commercial
applications, including (to name but a very few) aircraft design,
atomic reactor design, atomic weapons research, financial analysis,
calculation of income tax tables and other assorted tables, food
industry work, map making, optimum siting of power stations,
crystallography, spectroscopy, oil prospecting, and the simulation of
complex systems (the first traffic flow simulations were carried out
on the Pilot ACE). The last DEUCE went out of service in about 1970.
8. The ACE Family of Computers
The basic principles of Turing's ACE design were used in the G15
computer, built and marketed by the Detroit-based Bendix Corporation.
The G15 was designed by Harry Huskey, who spent 1947 at the NPL, working in
the ACE Section. The G15 was arguably the first personal computer. By
following Turing's philosophy of minimizing hardware in favour of
software, Huskey was able to make the G15 small enough (it was the
size of a large domestic refrigerator) and cheap enough to be
marketed as a single-user desk-side computer. Yet thanks to the
ACE-like design, the G15 was as fast as computers many times its
size. The first G15 ran in 1954. Over 400 were sold worldwide and the G15 remained in use until about
1970.
The full-scale ACE was inaugurated in 1958 (see chapter 24 The Big
ACE). Other
derivatives of Turing's ACE design include the MOSAIC (Ministry of Supply Automatic Integrator and Computer), which played a role in Britain's air defences during the Cold War period, the E.M.I. Business Machine, a relatively slow electronic computer with a large memory (designed for the shallow processing of large quantities of data that is typically demanded by business applications) and the low-cost transistorized Packard-Bell PB250.
The MOSAIC
The MOSAIC,
based on Version VII of Turing's logical design for the ACE, first
ran a program in 1952 or early 1953. William Chandler and Allen Coombs, Flowers' right-hand men from the
Colossus days, carried out the engineering design for the MOSAIC (see
chapter 18 First Attempt to Build the ACE: the Flowers Era). With a pulse rate of 570
kilo-Hertz (about half the speed of the ACE), the MOSAIC contained approximately 7000 valves
and 2000 semi-conductors (germanium diodes). Originally a high-speed memory of 96 mercury delay lines was
planned;
in the final form of the machine there were 64 long delay lines and a
handful of short delay lines, holding a total of 1030 40-digit
words. Of the various ACE-type computers that were built, the MOSAIC was
(apart from its slower pulse rate) the closest to Turing's conception
of the ACE.
The MOSAIC was installed in 1954 or early 1955 at the Royal
Radar Establishment in Malvern, where it was used to calculate aircraft trajectories from radar data,
in connection with anti-aircraft measures. (The details of the
computer's use are still classified.) Two mobile automatic
data-recorders operated in conjunction with a radar tracking system.
Each recorder involved approximately 2000 valves, with special
cathode-ray tube switches and pneumatic equipment to provide a record on
punched paper tape.
Given that two engineers working alone succeeded in completing the large MOSAIC (Coombs emphasized: 'it was just Chandler and I—we designed every scrap of that machine'), there is in our view little doubt that, given sufficient manpower, a computer reasonably close to Turing's Version VII of the ACE could have been operational in the very early 1950s. Thanks to their wartime involvement with Colossus, Chandler and Coombs possessed unrivalled expertise in large-scale digital electronics and had a substantial lead on everyone else in the field. Turing, of course, was well aware of this, but the Official Secrets Act prevented him from sharing his knowledge of Colossus with Darwin, Director of the National Physical Laboratory. Had he been able to do so, the NPL might have acted to boost the meagre resources available to Chandler and Coombs, so bringing a version of the ACE to life much sooner.
9. Turing and Artificial Intelligence (AI)

Dartmouth College, New Hampshire, venue of the Dartmouth Summer Research Project on Artificial Intelligence

Herb Simon and Al Newell, two of AI's pioneers
The myth
Artificial Intelligence is often said to have been born in the
mid-1950s in the U.S. For example:
Artificial Intelligence, conceived at Carnegie
Tech in the autumn of 1955, quickened by Christmas, and delivered on
Johnniac in the spring, made a stunning debut at the conference from
which it later took its name.
The AI program 'delivered on Johnniac' (a Californian copy of von Neumann's computer at the Institute for Advanced Study) was the Logic Theorist, written by Allen Newell, Herbert
Simon, and Cliff Shaw and demonstrated at a conference, the Dartmouth
Summer Research Project on Artificial Intelligence, held at Dartmouth
College, New Hampshire. The Logic Theorist was designed to prove theorems from Whitehead and
Russell's Principia Mathematica. In one case the proof devised by the Logic Theorist was several
lines shorter than the one given by Whitehead and Russell; Newell,
Simon, and Shaw wrote up the proof and sent it to the Journal of
Symbolic Logic. This was almost certainly the first paper to have
a computer listed as a co-author, but unfortunately it was
rejected.
The reality

Arthur Samuel, creator of the first AI program to run in the United States
In Britain the term 'machine intelligence' pre-dated 'artificial
intelligence', and the field of enquiry itself can be traced much
further back than 1955. If anywhere has a claim to be the birthplace
of AI, it is Bletchley Park. Turing was the first to carry out
substantial research in the area. At least as early as 1941 he was
thinking about machine intelligence—in particular the
possibility of computing machines that solved problems by means of
searching through the space of possible solutions, guided by what
would now be called 'heuristic' principles—and about the
mechanization of chess. At Bletchley Park, in his spare time, Turing discussed these topics
and also machine learning. He circulated a typescript concerning
machine intelligence among some of his colleagues. Now lost, this was undoubtedly the earliest paper in the field of AI.
The first AI programs ran in
Britain in 1951-52, at Manchester and Cambridge. This
was due in part to the fact that the first stored-program electronic
computers ran in Britain and in part to Turing's influence on the
first generation of computer programmers. Even in the U.S., the
Logic Theorist was not the first AI program to run. Arthur Samuel's
Checkers (or Draughts) player first ran at the end of 1952 on the IBM
701, IBM's first stored-program computer. In 1955 Samuel added learning to the program.
The Bombe

Working in a Bombe room at Outstation Eastcote. 'Menus' for outstation Bombes were received from Bletchley Park by teleprinter.

Christopher Strachey. Strachey's draughts (checkers) player was the first computer program to incorporate heuristics.

Burlington House, the venue of Turing's 1947 lecture

Charles Darwin, Director of the National Physical Laboratory

The first manifesto of Artificial Intelligence (1948)

The Turing test
| Judge: |
In the first line of your sonnet which reads ‘Shall I compare thee to a summer’s day’, would not ‘a spring day’ do as well or better? |
| Computer: |
It wouldn’t scan. |
| Judge: |
How about ‘a winter’s day’? That would scan all right. |
| Computer: |
Yes, but nobody wants to be compared to a winter’s day. |
| Judge: |
Would you say Mr. Pickwick reminded you
of Christmas? |
| Computer: |
In a way. |
| Judge: |
Yet Christmas is a winter’s day, and I do not think
Mr Pickwick would mind the comparison. |
| Computer: |
I don’t think you’re serious. By a winter’s day
one means a typical winter’s day, rather than a
special one like Christmas. |
Passing the Turing test: Turing's sample dialogue (from 'Computing Machinery and Intelligence')

Dietrich Prinz playing the Ferranti Mark I computer. Prinz wrote the first chess program to be implemented.

Strachey

Tony Oettinger in the courtyard of Clare College, Cambridge. Oettinger wrote the first learning programs.
The
Bombe is the first milestone in the history of machine intelligence.
Central to the Bombe was the idea of solving a problem
by means of a guided mechanical search through the space of possible
solutions. In this instance, the space of possible solutions
consisted of configurations of the Enigma machine (in another case it
might consist of configurations of a chess board). The Bombe's search
could be guided in various ways; one involved what Turing called the
'multiple encipherment condition' associated with a crib (described
in Chapter 6 of Turing's Treatise on the
Enigma, written in the second half of 1940; this chapter is in The Essential Turing and the entire Treatise is available online in The Turing Archive for the History of
Computing <http://www.AlanTuring.net/profs_book>). A search guided in this fashion, Turing said,
would 'reduce the possible positions to a number which can be tested
by hand methods'. A crib is a word or phrase
that the cryptanalyst believes might be part of the German message.
For example, it might be conjectured that a certain message contains
'WETTER FUR DIE NACHT' (weather for the night). Many Enigma networks
were good sources of cribs, thanks both to the stereotyped nature of
German military messages and to lapses of cipher security. One
station sent exactly the same message ('beacons lit as ordered') each
evening for a period of several months.
Modern AI researchers speak of the method of generate-and-test. Potential solutions to a given problem are
generated by means of a guided search. These potential solutions are
then tested by an auxiliary method to find out if any is actually a
solution. Nowadays in AI both processes, generate and test, are
typically carried out by the same program. The Bombe mechanized the
first process. The testing of the potential solutions (the 'stops')
was then carried out manually—by setting up a replica Enigma
accordingly, typing in the cipher text, and seeing whether or not
German words emerged.
Machine intelligence 1945-1948
In designing the ACE, machine intelligence was not far from Turing's
thoughts—he described himself as building 'a brain' and declared 'In working on the ACE I am more interested in the
possibility of producing models of the action of the brain than in
the practical applications to computing'. On page 16 of 'Proposed Electronic Calculator' he said:
'Can the machine play chess?' It could fairly
easily be made to play a rather bad game. It would be bad because
chess requires intelligence. We stated at the beginning of this
section that the machine should be treated as entirely without
intelligence. There are indications however that it is possible to
make the machine display intelligence at the risk of its making
occasional serious mistakes. By following up this aspect the machine
could probably be made to play very good chess.
(Turing's point was probably that the use of heuristic search brings
with it the risk of the machine's sometimes making mistakes.)
In February 1947 (in the rooms of the Royal Astronomical
Society in Burlington House, London)
Turing gave what is, so far as is known, the earliest public lecture
to mention computer intelligence, providing a breathtaking glimpse of
a new field. He described the human brain as a 'digital computing machine' and discussed the prospect of machines that act intelligently, learn,
and beat human opponents at chess. He stated that '[w]hat we want is
a machine that can learn from experience' and that '[t]he possibility
of letting the machine alter its own instructions provides the
mechanism for this'. The possibility of a computer's operating on and modifying its own
program as it runs, just as it operates on the data in its memory, is
implicit in the stored-program concept.
At the end of this lecture Turing set out what he later called
the 'Mathematical Objection' to the view that minds are machines.
This is now widely known as the Gödel argument, and has been
made famous by Roger Penrose. (In fact the objection originated with the mathematical logician Emil
Post, as early as 1921.)
Turing proposed an interesting and arguably correct solution to the
objection.
In the middle of 1947, with little progress on the physical
construction of the ACE, a thoroughly disheartened Turing applied for
a twelve-month period of sabbatical leave to be spent in Cambridge.
The purpose of the leave, as described by Darwin in July 1947, was to
enable Turing to
extend his work on the [ACE] still further
towards the biological side. I can best describe it by saying that
hitherto the machine has been planned for work equivalent to that of
the lower parts of the brain, and [Turing] wants to see how much a
machine can do for the higher ones; for example, could a machine be
made that could learn by experience? This will be theoretical work,
and better done away from here.
Turing left the NPL for Cambridge in the autumn of 1947 (see chapter
21 Turing Leaves the NPL).
In the summer of 1948 Turing completed a report describing the
outcomes of this research. It was entitled 'Intelligent Machinery'. Donald Michie recalls that Turing
was in a state of some agitation about its
reception by his superiors at N.P.L.: 'A bit thin for a year's time
off!'.
The headmasterly Darwin—who once complained about the 'smudgy'
appearance of Turing's work—was,
as Turing predicted, displeased with 'Intelligent Machinery',
describing it as a 'schoolboy's essay' and 'not suitable for publication'. In reality this far-sighted paper was the first manifesto of
Artificial Intelligence; sadly Turing never published it.
'Intelligent Machinery' is a wide-ranging and strikingly original
survey of the prospects of AI. In it Turing brilliantly introduced a
number of the concepts that were later to become central in AI, in
some cases after reinvention by others. These included the
logic-based approach to problem-solving, now widely used in expert
systems, and, in a brief passage concerning what he called 'genetical
or evolutionary search',
the concept of a genetic algorithm—important in both AI and Artificial Life. (The term 'genetic algorithm' was only introduced circa
1975.)
In the light of his work
with the Bombe, it is no surprise to find Turing hypothesizing in
'Intelligent Machinery' that 'intellectual activity consists
mainly of various kinds of search'. Eight years later the same hypothesis was put forward independently
by Newell and Simon and through their influential work became one of the principal tenets of AI. 'Intelligent Machinery'
also contains the earliest description of (a restricted form of) what
Turing was later to call the 'imitation game' and is now known simply
as the Turing test. It contains too his intriguing claim that the concept of intelligence is an 'emotional concept'.
The Turing test
In his 1950 article 'Computing Machinery and Intelligence' Turing
described an imitation game involving an interrogator and two
subjects, one male (A) and one female (B). The
interrogator communicates with A and B from a separate
room (nowadays this would probably be by means of a keyboard and
screen); apart from this the three participants have no contact with
each other. The interrogator's task is to find out, by asking
questions, which of A and B is the man. A's aim
is that the interrogator make the wrong identification. As to B,
Turing said 'The object of the game for the third player ... is to
help the interrogator. The best strategy for her is probably to give
truthful answers.'
Turing then asked, 'What will happen when a
machine takes the part of A in this game?'. The game is now one in which a computer imitates a human being (man
or woman). The interrogator's task is to discover which of A or B is the computer; to do so he or she is permitted to ask
any question (or put any point) on any topic. The computer is
allowed to do everything possible to force a wrong identification.
To assess the computer's performance, we ask:
Will the interrogator decide wrongly as often
when the [computer-imitates-human] game is played ...
as he does when the game is played between a man and a woman?
If the computer (in the computer-imitates-human game) does no worse
than the man (in the man-imitates-woman game), it succeeds in the
game. The ability to play the imitation game successfully is Turing's
proposed 'criterion for "thinking"'.The role of the man-imitates-woman game is frequently misunderstood, however.
The game is part of the protocol
for scoring the test. Will interrogators decide wrongly as often in
man-imitates-woman imitation games as they do in
computer-imitates-human games? This question, Turing said, replaces
the question 'Can machines think?'.
Some commentators claim that what Turing was doing in 'Computing
Machinery and Intelligence' was presenting a test in which the
computer is to impersonate a woman (rather than a human being), its
degree of success being compared with a male player's degree of
success at the same task. However, when describing his test in a
radio broadcast Turing said that '[t]he idea of the test is that the
machine has to try and pretend to be a man ... and it will pass only
if the pretence is reasonably convincing'; and in yet another presentation of the test he said simply that the
point of the test is to determine whether or not a computer can
'imitate a brain'.
The first AI programs
Both during and after the war Turing experimented with machine
routines for playing chess: in the absence of a computer, the
machine's behaviour was simulated by hand, using paper and pencil. In
1948 Turing and David Champernowne, the mathematical economist,
constructed the loose system of rules dubbed the 'Turochamp'. Champernowne reported that his wife, a beginner at chess, took on
the Turochamp and lost. Turing began to program the Turochamp for
the Manchester Ferranti Mark I but unfortunately never completed the
task. He later published a classic early article on chess programming.
Dietrich Prinz, who worked for Ferranti, wrote the first chess
program to be implemented. It ran in November 1951 on the Ferranti Mark I. Unlike the Turochamp, Prinz's program could not play a complete game
and operated by exhaustive search rather than under the guidance of
heuristics. Prinz 'learned all about programming the Mark I computer
at seminars given by Alan Turing and Cecily Popplewell'. Like Turing, he wrote a programming manual for the Mark I. Prinz also used the Mark I to solve logical problems. (In 1949 and
1951 Ferranti built two small experimental special-purpose computers
for theorem-proving and other logical work.)
Christopher Strachey's Draughts Player was—apart from Turing's
'paper' chess-players—the first AI program to use heuristic
search. He coded it for the Pilot Model ACE in May 1951. Strachey's first attempt to get his program running on the
Pilot ACE was defeated by coding errors. When he returned to the NPL
with a debugged version of the program, he found that a major
hardware change had been made, with the result that the program would
not run without substantial revision. He finally got his program working on the Ferranti Mark I in mid-1952, with Turing's encouragement and utilizing the latter's recently
completed Programmer's Handbook. By the summer of 1952 the program could play a complete game of
draughts at a reasonable speed. The essentials of Strachey's program were taken over by Arthur Samuel in the U.S.
The first AI programs to incorporate learning, written by Anthony
Oettinger at the University of Cambridge, ran in 1951. Oettinger wrote his 'response learning programme' and 'shopping
programme' for the Cambridge EDSAC computer.
Oettinger was considerably influenced by Turing's views on machine
learning,
and suggested that the shopping program—which simulated the
behaviour of 'a small child sent on a shopping tour'—could
pass a version of the Turing test in which 'the questions are
restricted to ... the form "In what shop may article j be
found?" '.
Turing's anticipation of connectionism

Fragment of a large Turing Net

A modern connectionist networkXXXXXXXXXXXXXXXXXX
Turing did not only invent the concept of the stored-program digital computer; he also pioneered the idea of computing by artificial neural networks. The major part of his 1948 paper 'Intelligent Machinery' is a discussion, anticipating the modern field of connectionism, of what Turing called 'unorganised machines'.
Standard digital computers are superb number crunchers. Ask them to predict a rocket's trajectory or calculate the financial figures for a large multinational corporation, and they can churn out the answers in seconds. But seemingly simple actions that people routinely perform, such as recognising a face or reading handwriting, have proved extremely difficult to program. Perhaps the networks of neurons that make up the brain have a natural facility for such tasks that standard computers lack.
Connectionism, still in its infancy, is the science of computing with networks of neurons. Researchers typically simulate the artificial neurons and their interconnections using an ordinary digital computer—just as an engineer may use a computer to simulate an aircraft wing or a weather analyst to simulate a storm system. Connectionism came to the fore in the mid-1980s, when a group based at the University of California at San Diego reported some striking experiments. In one, an artificial neural network learned to form the past tenses of English verbs. The network learned to respond correctly even to irregular verbs not previously encountered, such as ‘weep’ (wept) and ‘cling’ (clung)! The term 'connectionism' highlights the fact that what an artificial neural network learns is stored in its pattern of inter-neural connections.
Turing's unorganised computing machines had been forgotten until we published our paper 'On Alan Turing’s Anticipation of Connectionism' in 1996, and then in 1999 an article in Scientific American on Turing's forgotten ideas on neural computation.Turing described three types of unorganised machine. His A-type and B-type unorganised machines consist of randomly connected two-state 'neurons' whose operation is synchronised by means of a central digital clock; we call these 'Turing Nets'. It is Turing's discussion of B-types that anticipates modern connectionism. Turing's P-type unorganised machines are not neuron-like but are modified Turing machines: they have, Turing said, 'two interfering inputs, one for "pleasure" or "reward" ... and the other for "pain" or "punishment"'. Turing studied P-types in the hope of discovering procedures for 'training' a machine to carry out a task. It is a P-type machine that Turing was speaking of when, in the course of his famous discussion of strategies for building machines to pass the Turing test, he said 'I have done some experiments with one such child-machine, and succeeded in teaching it a few things'.
Warren McCulloch

Walter Pitts
B-types too can be taught, and the most significant aspect of Turing's discussion of B-types is undoubtedly his idea that an initially random network can learn to perform a specified task by means of what he described as 'interfering training':
Many unorganised machines have configurations such that if once that configuration is reached, and if the interference thereafter is appropriately restricted, the machine behaves as one organised for some definite purpose.
In a B-type, the training process renders certain neural pathways effective and others ineffective—training hones the network for a specific task by selectively disabling and enabling connections.
Turing theorized that 'the cortex of the infant is an unorganised machine, which can be organised by suitable interfering training', and he described A-type unorganised machines as 'about the simplest model of a nervous system with a random arrangement of neurons'. He found 'this picture of the cortex as an unorganised machine ... very satisfactory from the point of view of evolution and genetics'. Turing had no doubts concerning the significance of his unorganised machines. Of Turing Nets, he said
[M]achines of this character can behave in a very complicated manner when the number of units is large ... It would therefore be of very great interest to find out something about their behaviour.
In its treatment of learning, Turing's 'Intelligent Machinery' goes importantly beyond the famous 1943 paper on neural networks by McCulloch and Pitts. McCulloch and Pitts gave only a perfunctory discussion of learning, saying no more than that the mechanisms supposedly underlying learning in the brain—they specifically mentioned the formation of new inter-neural connections and changes in the 'threshold' at which a neuron 'fires'—can be mimicked by means of nets whose connections and thresholds are fixed. Turing’s idea of using supervised interference to train an initially random arrangement of neurons is nowhere prefigured. It is also noteworthy that McCulloch stressed the extent to which his and Pitts’ 1943 paper on neural networks is indebted to Turing's 1936 paper 'On Computable Numbers'. McCulloch said in 1948: 'I started at entirely the wrong angle ... and it was not until I saw Turing’s paper that I began to get going the right way around, and with Pitts’ help formulated the required logical calculus. What we thought we were doing (and I think we succeeded fairly well) was treating the brain as a Turing machine.'

Pioneer of connectionism Frank Rosenblatt, with the image sensor (left) of the Mark I Perceptron

The Mark I Perceptron
Turing also envisaged the procedure—nowadays used extensively by connectionists—of programming training algorithms into a computer simulation of an unorganised machine. In modern connectionism, repeated applications of a training algorithm (such as the backprop or 'back propagation' algorithm) cause the required pattern of connectivity to develop gradually within the network during the training phase. Turing had no algorithm for training his B-types, however. He saw the development of training algorithms for unorganised machines as a central problem. With characteristic farsightedness Turing ended his discussion of unorganised machines by sketching the research programme that connectionists are now pursuing:
I feel that more should be done on these lines. I would like to investigate other types of unorganised machines ... When some electronic machines are in actual operation I hope that they will make this more feasible. It should be easy to make a model of any particular machine that one wishes to work on within such a UPCM [universal practical computing machine] instead of having to work with a paper machine as at present. If also one decided on quite definite 'teaching policies' these could also be programmed into the machine. One would then allow the whole system to run for an appreciable period, and then break in as a kind of 'inspector of schools' and see what progress had been made.
Turing was unable to pursue his research into unorganised machines very far. At the time, the only electronic stored-program computer in existence was the tiny Manchester Baby. By the time Turing had access to the Ferranti Mark I, in 1951, his interests had shifted and he devoted his time to modelling biological growth. At the National Physical Laboratory, Turing's ideas on learning were pursued by his colleagues Donald Davies and Michael Woodger. Their Cybernetic Model, constructed in 1949, was a hardware simulation of six Boolean neurons. In a demonstration on BBC TV in 1950, the Cybernetic Model mimicked simple learning in an octopus.
In the year of Turing’s death (1954) two researchers at MIT, Wesley Clark and Belmont Farley, succeeded in running the first computer simulations of neural networks. Clark and Farley were unaware of Turing’s earlier work and their neural architecture was quite different from his: Clark and Farley used 'weighted' connections between neurons, as is now usual in connectionism. Clark and Farley were able to train their networks—which contained a maximum of 128 neurons—to recognise simple patterns. In addition, they discovered that the random destruction of up to 10% of the neurons in a trained network does not affect the network's performance at its task—a feature reminiscent of the brain's ability to tolerate damage.
The work begun by Clark and Farley was developed very considerably by Frank Rosenblatt at Cornell University, who built neural network-like computers that he called 'Perceptrons'. Rosenblatt used the term 'connectionist' for the approach and his 1962 book Principles of Neurodynamics became the reference work for the emerging field. Modern connectionists regard Rosenblatt as the founding father of their approach, and it is still not widely realised that Turing wrote a blueprint for much of the connectionist project as early as 1948.
10. Turing and Artificial Life (A-Life)

Pigmentation pattern in a seashell, generated by a modern variant of Turing's morphogenesis process. (A modification of Turing's 1952 reaction-diffusion process by H. Meinhardt.)
algorithmicbotany.org
Pattern of growth on a flat surface, generated by M. Eden's variant of Turing's reaction-diffusion process.
algorithmicbotany.org

Pattern of growth produced by
diffusion-limited aggregation (DLA), another variant of Turing's reaction-diffusion.
algorithmicbotany.org
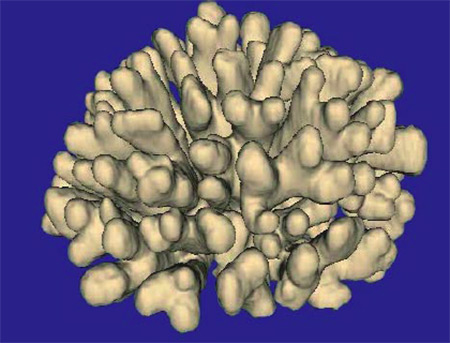
Sponge-like growth produced by DLA

In his final years Turing worked on (what since 1987 is called)
Artificial Life (A-Life). The central aim of Artificial Life is a
theoretical understanding of naturally-occurring biological life—in
particular of the most conspicuous feature of living matter, its
ability to self-organise (i.e. to develop form and structure
spontaneously). A-Life characteristically makes use of computers to
simulate living and life-like systems. Christopher Langton, who
coined the term 'Artificial Life', wrote
Computers should be thought of as an important
laboratory tool for the study of life, substituting for the array of
incubators, culture dishes, microscopes, electrophoretic gels,
pipettes, centrifuges, and other assorted wet-lab paraphernalia, one
simple-to-master piece of experimental equipment.
Turing was the first to use computer simulation to investigate a
theory of 'morphogenesis'—the development of organisation and
pattern in living things. He began this investigation as soon as the first Ferranti Mark I to
be produced was installed at Manchester University.
In February 1951 Turing wrote:
Our new machine is to start arriving on Monday.
I am hoping as one of the first jobs to do something about 'chemical
embryology'. In particular I think one can account for the appearance
of Fibonacci numbers in connection with fir-cones.
Shortly before the Ferranti computer arrived, Turing wrote about his
work on morphogenesis in a letter to the biologist J. Z. Young. The
letter connects Turing's work on morphogenesis with his interest in
neural networks, and to some extent explains why he did not follow up
his suggestion in 'Intelligent Machinery' and use the Ferranti
computer to simulate his unorganised machines.
I am afraid I am very far from the stage where I
feel inclined to start asking any anatomical questions [about the
brain]. According to my notions of how to set about it that will not
occur until quite a late stage when I have a fairly definite theory
about how things are done.
At present I am not working on the problem at
all, but on my mathematical theory of embryology ...
This is yielding to treatment, and it will so far as I can see, give
satisfactory explanations of-
i) Gastrulation.
ii) Polyogonally symmetrical structures, e.g.,
starfish, flowers.
iii) Leaf arrangement, in particular the way the
Fibonacci series (0, 1, 1, 2, 3, 5, 8, 13, ... ) comes to be
involved.
iv) Colour patterns on animals, e.g., stripes,
spots and dappling.
v) Patterns on nearly spherical structures such
as some Radiolaria, but this is more difficult and doubtful.
I am really doing this now because it is
yielding more easily to treatment. I think it is not altogether
unconnected with the other problem. The brain structure has to be one
which can be achieved by the genetical embryological mechanism, and I
hope that this theory that I am now working on may make clearer what
restrictions this really implies. What you tell me about growth of
neurons under stimulation is very interesting in this connection. It
suggests means by which the neurons might be made to grow so as to
form a particular circuit, rather than to reach a particular place.
In June 1954, while in the midst of this groundbreaking work, Turing
died. He left a large pile of handwritten notes concerning
morphogenesis, and some programs. This material is still not fully understood.
SPACER
11. The Manchester Computer

The Manchester ‘Baby’. The world's first electronic stored-program computer, the Baby ran its first program in June 1948, in the Computing Machine Laboratory at the University of Manchester. Freddie Williams (right) and Tom Kilburn pose in front of the cathode ray display.
Turing and the NPL lost the race to build the world's first stored-program electronic digital computer—an honour that went to the University of Manchester, where the 'Manchester Baby' ran its first program on 21 June 1948. As its name implies, the Baby was a very small computer, and the news that it had run what was only a tiny program—just 17 instructions long—for a mathematically trivial task was (in Woodger's words) 'greeted with hilarity' by Turing's group.
The Manchester computer project was the brainchild of Turing's friend and colleague Max Newman, whose section at Britain's wartime codebreaking headquarters, Bletchley Park, had contained 10 Colossus computers working around the clock to break German codes. Newman, like von Neumann in the United States, was profoundly influenced by Turing's pre-war conception of a universal computing machine. It was in Newman's Computing Machine Laboratory that the Baby—the first real-world universal Turing machine—came to life.

Max Newman. Head of the Tunny-breaking section called the 'Newmanry', Newman was in charge of the Colossi. He went on to found the Computing Machine Laboratory at Manchester University.
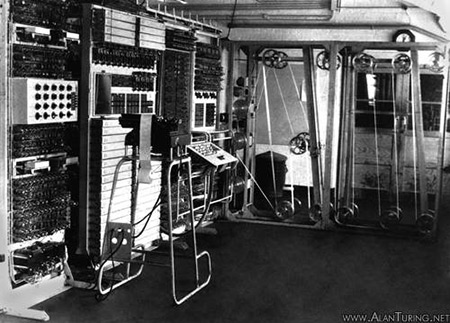
Colossus X. In the foreground is the automatic typewriter for output. The large frame to the right (the 'bedstead') held two message tapes. As one job was being run, the tape for the next job would be loaded onto the bedstead, so saving time.
It was no coincidence that as soon as the war ended Turing and Newman both embarked on projects to create a universal Turing machine in hardware. Even in the midst of the attack on Tunny, Newman was thinking about the universal Turing machine. When Flowers was designing Colossus, Newman showed him Turing’s 1936 paper about the universal machine ('On Computable Numbers'), with its key idea of storing symbolically-encoded instructions in memory. By 1944 Newman was looking forward to setting up his own electronic computer project as soon as the war was over. As he said in a letter to von Neumann (quoted in chapter 2 Codebreaking in World War II), it was just a question of waiting until he 'got out' of Bletchley Park.
Moreover, it had been Newman who, in a lecture in Cambridge in 1935, had launched Turing on the research that led to the universal Turing machine. In the lecture, Newman had defined a constructive process as one that a machine can carry out. He explained in an interview
I believe it all started because [Turing] attended a lecture of mine on foundations of mathematics and logic ... I think I said in the course of this lecture that what is meant by saying that [a] process is constructive is that it’s a purely mechanical machine — and I may even have said, a machine can do it.
And this of course led [Turing] to the next challenge, what sort of machine, and this inspired him to try and say what one would mean by a perfectly general computing machine.
After Newman learned of Turing's universal computing machine early in 1936, he developed an interest in computing machinery which he described as being at that time 'rather theoretical'. Turing himself was interested right from the start in building a universal computing machine, but he knew of no suitable technology. It was not until his and Newman's Bletchley days that the dream of building a miraculously fast all-purpose electronic computer took hold of them.
Historians who did not know of Colossus tended to assume that Turing and Newman inherited their vision of large-scale electronic computing machinery from the ENIAC group in the U.S. In reality, Colossus was the link between Turing's pre-war work and his and Newman's post-war projects to build an electronic stored-program computer. (Flowers saw the ENIAC just after the war. In his opinion the ENIAC was just a number cruncher—Colossus, with its elaborate facilities for logical operations, was 'much more of a computer than ENIAC', he said.)
Newman had laid plans for his Computing Machine Laboratory following his appointment to the Fielden Chair of Mathematics at Manchester in September 1945. His formidable talent as an organiser, honed in the Newmanry, was now brought to bear on the problem of designing and constructing an electronic stored-program computer. Newman applied to the Royal Society for a sizeable grant (approved in May 1946) to develop such a machine. Parts of the Colossi were transferred from Bletchley Park to Manchester, including some of the electronic panels—although not before every indication of their original purpose had been removed! The first work on the Baby computer made use of the 'bedstead' from a Colossus, the giant iron frame (right) that held the message tape. 'It reminds me of Adam's rib', said Jack Good, one of the Newmanry codebreakers who moved with Newman to Manchester.

Freddie Williams

A Williams Tube. The cathode ray tube is better known in its role of television tube.

Bits stored on the face of a cathode ray tube
At Bletchley, Newman had been chief executive of a project with a staff of over 300. He initiated and oversaw the creation of a dazzling array of machines, all lying at the frontier of current technology (not only the Robinsons and the Colossi—for descriptions of other Newmanry machines, see General Report on Tunny and Colossus: The Secrets of Bletchley Park's Codebreaking Computers). Newman, himself no engineer, achieved these outstanding successes by the skilful use of a simple principle: get the right engineers involved, explain to them what needs to be done, and let them get on with it. (Once Newman had 'placed his trust in people he cut them loose to manage according to their own judgement' said Donald Michie, Newman's assistant at Bletchley Park.) Not surprisingly, Newman followed the same method at Manchester. He educated Frederic Williams—who was recruited to Manchester University from the Telecommunications Research Establishment (TRE)—in the fundamentals of the stored-program computer. At TRE during the war Williams and his assistant Tom Kilburn had worked on radar and were experts in electronic circuit design. (They themselves knew nothing of Colossus. Williams did not hear about what had gone on at Bletchley until 'we were actually active in the computer field, when they thought they had something to gain from us'. This was in 1952, when Williams was consulted by GCHQ and was invited to their headquarters, which by then had shifted from Bletchley Park to Eastcote near London.)
At the time he left TRE for Manchester in 1946, Williams was in the process of developing a method for storing patterns of zeros and ones on the face of a cathode ray tube—an idea that, with Kilburn’s help, was rapidly to lead to the type of high-speed random access memory (RAM) known as the Williams Tube. (Although, since Williams and Kilburn shared the later patents and shared the royalties equally, the name 'Williams-Kilburn Tube' would be more appropriate.) The Williams Tube was a mainstay of early computing. Computers using Williams Tube memory included not only those built at the University of Manchester and by the Manchester engineering company Ferranti, but also the SWAC at the University of California at Los Angeles, the Whirlwind I at the Massachusetts Institute of Technology, the IAS computer at Princeton University, the IBM 701, TRE's own TREAC (Telecommunications Research Establishment Arithmetic Computer)—and the ORDVAC, ORACLE, ILLIAC, MANIAC and other engagingly named computers.
It was in the summer of 1946, at about the same time that the Royal Society approved Newman’s grant, that Williams began his experiments at TRE on cathode ray tube storage. Williams explained how it was that he came to be working on the problem of computer memory:
[O]nce [the German Armies] collapsed ... nobody was going to care a toss about radar, and people like me ... were going to be in the soup unless we found something else to do. And computers were in the air. Knowing absolutely nothing about them I latched onto the problem of storage and tackled that.
Newman learned of Williams’ work. With his friend Patrick Blackett (Langworthy Professor of Physics at Manchester and one of the most powerful figures in the University) Newman had a hand in the appointment of the 35-year-old Williams to the recently vacated Chair of Electro-Technics at Manchester. Both Newman and Blackett were members of the appointing committee. Once appointed Williams secured Kilburn's secondment to his new department at Manchester.
Williams had succeeded in storing a single binary digit in the autumn of 1946, a few weeks before he left TRE in December for the University of Manchester. By this time Newman was already in possession of his Royal Society grant, but his Computing Machine Laboratory was little more than an empty room. 'So it was a very fruitful opportunity for collaboration', said Williams. Williams’ description of the Computing Machine Laboratory is vivid: 'It was one room in a Victorian building whose architectural features are best described as "late lavatorial". The walls were of brown glazed brick and the door was labelled "Magnetism Room"'. Here Kilburn and Williams built the Manchester Baby. The first program, stored on the face of a Williams Tube as a pattern of dots, was inserted manually, digit by digit, using a panel of switches. 'A small electronic digital computing machine has been operating successfully for some weeks in the Royal Society Computing Machine Laboratory', wrote Williams and Kilburn in the letter to Nature announcing their success to the world.
The regeneration principle

Turing

Aquarius. 'This form of memory is similar to random access storage on the screen of a cathode ray tube, as in the Williams tube memory', says Harry Fensom, one of the creators of Aquarius.
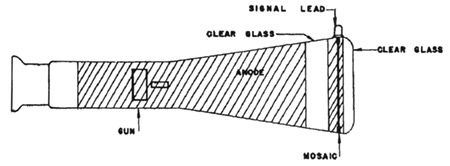
An iconoscope

MIT Radiation Lab

F. C. Williams

A Williams Tube in its case. The pickup plate is visible inside the lid of the case.

TRE (Telecommunications Research Establishment) in Malvern, where Williams achieved his breakthrough

Williams

Williams
Turing had mentioned cathode ray tube storage on page 48 of 'Proposed Electronic Calculator', saying that this was '[m]uch the most hopeful scheme' for storage. In effect Turing anticipated the Williams Tube in some detail, six months or more before Williams first heard of the problem of digital storage. Turing wrote:
It seems probable that a suitable storage system can be developed without involving any new types of tube, using in fact an ordinary cathode ray tube with tin-foil over the screen to act as a signal plate. It will be necessary to furbish up the charge pattern from time to time, as it will tend to become dissipated. ... If we were always scanning the pattern in a regular manner as in television this would raise no serious problems. As it is we shall have to provide fairly elaborate switching arrangements to be applied when we wish to take off a particular piece of information. It will be necessary to ... switch to the point from which the information required is to be taken, do some scanning there, replace the information removed by the scanning, and return to refurbishing from the point left off. ... None of this involves any fundamental difficulty, but no doubt it will take time to develop.
'Furbishing up' (i.e. regenerating) the stored pattern was certainly the central problem. The pattern would persist for a time, but unless a means could be found to regenerate it, the stored information would eventually disappear. Moreover, scanning the stored pattern in order to read it also tended to destroy it.
The earliest regenerative memories had used electrical capacitors as the storage units. At Bletchley Park during the war the codebreaking machine Aquarius was equipped with a regenerative memory consisting of a large bank of capacitors (details were not declassified until 2000). Data read in from a punched paper tape was stored as a pattern of electrical charge, a charged capacitor representing the digit 1 and an uncharged capacitor 0. Since the charge would gradually leak away, the pattern was regenerated by means of a periodic pulse that topped up those capacitors already containing some charge—a contemporary account described the process of regeneration as proceeding 'according to the rule "to him that hath shall be given"'. The memory could store in excess of 1500 binary digits (315 teleprinter characters expressed in 5-bit code). On the other side of the Atlantic, three or four years earlier, John Atanasoff had also built a capacitor-based regenerative memory capable of storing 1500 bits, for use in his largely unsuccessful 300-valve electronic calculator.
The cathode ray tube, already in widespread use in the television industry and elsewhere, seemed in theory a better bet than the capacitor as the basis for a high-speed computer memory. Early unsuccessful experiments with cathode ray tube storage focussed, not on the ordinary type of tube recommended by Turing and later employed by Williams, but on a more complicated type of tube called an iconoscope. The iconoscope was a light-sensitive tube used in television cameras; it converted the optical image produced by the camera lens into electricity. When the light image fell on the outside surface of a plate (or 'mosaic') at the end of the iconoscope, a pattern of electrical charge was created; this pattern was read by a scanning beam of electrons inside the tube and converted into electrical current. Instead of using light, the early storage experiments placed a pattern on the iconoscope's plate by means of the electron beam that read the pattern once stored. These experiments were carried out at the Radiation Laboratory of the Massachusetts Institute of Technology, and the aim was to store, not digital information for use in electronic computers, but analogue information—lines and shapes—in connection with echo cancellation in radar. The plan was to store a radar trace and then 'subtract' it from subsequent traces, so enabling the operator to see only moving objects.
The problem was that storage could not be achieved for more than very short periods. A Radiation Laboratory account dated February 1946 reported storage of a spiral pattern 'for nearly a second under suitable conditions'. No satisfactory means was found of prolonging storage. Williams (a leading expert on radar) was shown the storage experiments during a visit to the Radiation Laboratory in June 1946. He later summed up what he saw there: 'You could put your signal on, and provided you went and looked for it again within half a second or so, there it was—but if you hoped to find it the next day, there it was gone.'
Von Neumann had mentioned the iconoscope as a possible means of achieving high-speed digital storage in 'First Draft of a Report on the EDVAC' (1945). He was aware of the need to regenerate the stored information and suggested what became known as the 'two-tube method'. Two iconoscopes were to be connected together and the stored information would be regenerated by means of continually passing it back and forth between the two tubes. Whether von Neumann learned of the possibility of using the iconoscope as a regenerative memory from Presper Eckert (engineering designer of the ENIAC and EDVAC), or whether perhaps Eckert learned of the idea from von Neumann, is unknown. At any rate, Eckert lectured extensively on the possibilities of cathode ray tube storage at the Moore School in the summer of 1946. Kite Sharpless, one of Eckert's team at the Moore School (and later director of the EDVAC project) had already experimented earlier that year with storing bits on the face of a standard cathode ray tube, using a metal foil placed over the screen as a target plate. The basic set-up was very similar to that previously outlined by Turing. However, no method of regeneration was discovered and the experiments did not lead anywhere. The Moore School team was also interested in the two-tube method of regeneration, but the difficulty was to make the method work in practice. At the MIT Radiation Lab attempts were made to store analogue traces using the two-tube method, but these too were unsuccessful.
At TRE Williams decided to tackle the problem of digital storage. He had seen the unsuccessful attempt at digital storage by Eckert's team at the Moore School, and during his visit to the Radiation Lab had also seen the two-tube experiment aimed at analogue storage. Kilburn explained:
What happened was that Freddie went to the States and he saw cathode ray tube attempts to store analogue signals. This was a two-tube system. Freddie came back and set [the experiment] up himself so that he could see what they were doing. So he set up this experiment of two tubes in which analogue signals were to be passed from one tube to another and vice versa, in order to regenerate analogue signals.
Williams never managed to get the two-tube system to work, but during his efforts to adapt the two-tube system to digital storage he discovered the phenomenon that would make cathode ray tube storage a reality, the anticipation pulse. In the course of his attempt to store a straight line with a gap in it—effectively one bit—on the face of the cathode ray tube, Williams observed that when the electron beam was turned off at the start of the gap, an electrically charged 'marker' was naturally left on the screen. The marker spread out a little over the screen and the result was that when the scanning beam returned to read the information on the screen, the marker provided advance warning of the point where the beam had turned off. This advance warning—the anticipation pulse—could be used to control the regeneration of the line-plus-gap, by turning the regenerating beam off at the point where the gap began. (The marker was an artefact of secondary electron emissions and the whole anticipation pulse effect was a quirk of the phosphorescent substance used to coat the face of the tube.) One off-the-shelf cathode ray tube was all that was required to make this method work, and Williams successfully stored one bit shortly after his discovery of the anticipation pulse.
In the end, the anticipation pulse was not used in the Baby computer. Kilburn soon discovered other methods of regeneration. There was, in any case, a logical lesson to be learned from the anticipation pulse, as Williams remarked: 'although the anticipation pulse ... was the real breakthrough, as soon as you spotted that, you realised that you can reorganise operations ... you go and look at a spot and say "what's there?", all right that's there, so you put it back.' The anticipation pulse was not needed.
Williams and Kilburn reflected in 1953 that 'it is amazing how long it took to realize the fact that if one can read a record once, then that is entirely sufficient for storage, provided that what is read can be immediately rewritten in its original position.' Turing had realised this in 1945, and stated the idea very clearly in 'Proposed Electronic Calculator' (in the passage quoted earlier). Williams was sent a copy of 'Proposed Electronic Calculator' by the National Physical Laboratory in October 1946—about the time of his discovery of the anticipation pulse (October or November 1946). He need only have glanced at the table of contents of 'Proposed Electronic Calculator' in order to see the irresistible chapter title 'Alternative Forms of Storage'.Turing described the regeneration problem from a logician's point of view. His words ('It will be necessary to ... switch to the point from which the information required is to be taken, do some scanning there, [then] replace the information removed by the scanning …') might well have helped Williams towards an appreciation of the logical lesson that reading and rewriting are together sufficient to solve the problem of regeneration.

Interior view of the TRE computer TREAC. TREAC contained a Williams Tube memory.
Setting the record straight

Newman as a young Fellow of St. John's College, Cambridge

Newman in 1940, two years before he joined the codebreakers at Bletchley Park

Newman on a mountain in Wales, circa 1948
At the time of the Baby and its successor, the Manchester Mark I, Williams and Kilburn were given too little credit by the mathematicians at Manchester. Williams and Kilburn, who had translated the logico-mathematical idea of the stored-program computer into hardware, were regarded as excellent engineers but not as 'ideas men'. Nowadays the tables have turned too far and the triumph at Manchester is usually credited to Williams and Kilburn alone. Fortunately the words of the late Freddie Williams survive to set the record straight:
Now let's be clear before we go any further that neither Tom Kilburn nor I knew the first thing about computers when we arrived in Manchester University. We'd had enough explained to us to understand what the problem of storage was and what we wanted to store, and that we'd achieved, so the point now had been reached where we'd got to find out about computers. ... Newman had already got a grant from the Royal Society to build a computer but had not in fact yet embarked on the problem of building it. Nor indeed was Newman, who was a mathematician, the right sort of person to build a computer. So it was a very fruitful opportunity for collaboration between the maths department and the electrical engineering department — and Newman explained the whole business of how a computer works to us. ... [The building of the Baby computer] was a straightforward process: we had the method of storage; we had instructions from Newman as to what facilities needed to be provided.
Historians have either ignored or underestimated the roles played by Turing and Newman in the development of the stored-program computer at Manchester. Even Newman's own account of the matter is—characteristically—self-effacing. Williams, however, is perfectly clear in attributing credit:
Tom Kilburn and I knew nothing about computers ... Professor Newman and Mr A. M. Turing ... knew a lot about computers ... They took us by the hand and explained how numbers could live in houses with addresses ...
Going by Williams' later description (quoted below), Newman's explanation of the stored-program computer to Williams and Kilburn—which took place early in 1947—resembled an account that he gave in an address to the Royal Society on 4 March 1948 and which was captured in print:
In modern times the idea of a universal calculating machine was independently [of Babbage] introduced by Turing ... There is provision for storing numbers, say in the scale of 2, so that each number appears as a row of, say, forty 0's and 1's in certain places or 'houses' in the machine. ... Certain of these numbers, or 'words' are read, one after another, as orders. In one possible type of machine an order consists of four numbers, for example 11, 13, 27, 4. The number 4 signifies 'add', and when control shifts to this word the 'houses' H11 and H13 will be connected to the adder as inputs, and H27 as output. The numbers stored in H11 and H13 pass through the adder, are added, and the sum is passed on to H27. The control then shifts to the next order. In most real machines the process just described would be done by three separate orders, the first bringing ‹H11› (= content of H11) to a central accumulator, the second adding ‹H13› into the accumulator, and the third sending the result to H27; thus only one address would be required in each order. ... A machine with storage, with this automatic-telephone-exchange arrangement and with the necessary adders, subtractors and so on, is, in a sense, already a universal machine ...
Here Newman's explanation presents both Turing's three-address format for instructions (source 1, source 2, destination, operation) and also a single-address format (address, operation) associated with a central 'accumulator'. (An accumulator is a storage unit able to form the sum of an incoming number and the number already stored; this sum then replaces the previous content of the store.) Newman's mention of the single-address format and a central accumulator was a reference to the centralised design championed by von Neumann in 'First Draft of a Report on the EDVAC' (1945) and 'Preliminary Discussion of the Logical Design of an Electronic Computing Instrument' (1946) (see further chapter 12 The Manchester Computer and John von Neumann). The three-address format was introduced by Turing in Versions VI and VII of the ACE design (see 'The Turing–Wilkinson Lecture Series' in Alan Turing's Automatic Computing Engine). From Turing's point of view, its use enabled one instruction to replace three single-address instructions, so giving greater speed.
Newman went on to describe program storage ('the orders shall be in a series of houses X1, X2, ...') and conditional branching ('A conditioned change of control is needed, i.e. the capacity to change control to an arbitrarily specified order if (say) a certain number is positive, but to go on to the next order otherwise'). Newman said: 'The provision for change of control, and above all for conditional change of control according to the sign of a certain number, is the most characteristic part of these machines'. Elsewhere he emphasised the connection with Colossus: Colossus 'had a very characteristic feature which is sometimes taken to be the characteristic of a general computing machine; and that is, that it looks at the answer to what is done so far and does one thing if the answer is 0, say, and another thing if the answer is 1, and this is a very important step—and this step was taken in Colossus'.
In his Royal Society lecture Newman then summed up the essentials of a stored-program computer, probably in much the same words that he used when giving his 'few lectures' the previous year to the engineers:
From this highly simplified account it emerges that the essential internal parts of the machine are, first, a storage for numbers (which may also be orders). ... Secondly, adders, multipliers, etc. Thirdly, an 'automatic telephone exchange' for selecting 'houses', connecting them to the arithmetic organ, and writing the answers in other prescribed houses. Finally, means of moving control at any stage to any chosen order, if a certain condition is satisfied, otherwise passing to the next order in the normal sequence. Besides these there must be ways of setting up the machine at the outset, and extracting the final answer in useable form.

The Manchester computer in Newman's Computing Machine Laboratory

The Manchester 'Baby' computer
As Williams and Kilburn described it, the basic rhythm of the Baby was 'four beats to the bar'. The single-line store C.I. (for 'control instruction') holds the address at which the next instruction is stored in S. In the first beat, this address is transferred to the staticisor (in the Princeton idiolect, the staticisor was called the 'function table register'). The staticisor both controls the flow of information to and from the store, and controls the execution of the instructions in the program. Also in the first beat, 1 is added to the address in C.I., in preparation for the start of the next bar (or 2 is added if, in the next bar, the next instruction in the store is to be skipped). In the second beat, the staticisor selects the line of S designated by the address received from C.I., and routes the instruction which is stored there into the single-line store P.I. (for 'present instruction'). An instruction consists of a single address followed by a numerical code designating an operation (called the function code); and, correspondingly, the staticisor consists of two blocks of equipment, the s-block, which accesses the store S by means of an address (as just described), and the f-block, which causes the operation specified by the function code to be carried out. In the third beat, the present instruction is fed from P.I. back into the staticisor, so that in the next beat the s-block and f-block can do their work. In the fourth beat, the s-block accesses the number stored in the line of S whose address appears in the instruction, and the f-block causes the operation specified by the function code to be executed—e.g. the operation of subtracting the number in line x of S from the number in the accumulator and storing the result in the accumulator. After the fourth beat of the bar comes the first beat of the next bar. (The diagram indicates the potential for adding a number from S to the number stored in C.I., a facility not included in the original Baby but soon incorporated.)
Newman had explained to the engineers what they needed to build. And so (although this is not what orthodox histories of the Manchester computer maintain) credit for the Manchester computer—tellingly called the 'Newman–Williams machine' by Huskey in a report written shortly after his visit to the Manchester project in 1947—belongs not only to Williams and Kilburn but also to Newman. It is also clear that the influence on Newman of Turing's 1936 paper, and of Flowers' Colossus, was crucial. A separate thread of the story, Turing's influence on Kilburn, is disentangled below. Turing's contribution to the development of Kilburn's design for the first computer has not been recognised in orthodox histories of the Manchester project.
In a letter written in 1972, Williams described in some detail what he and Kilburn were told by Newman. Williams said that this was the 'first information' that he received about the organisation of computers, although (as we will explain) Kilburn had in fact already received a thorough grounding in the basics of computer design in lectures given by Turing in London. Williams said, accurately enough, that the Baby machine was an 'embodiment' of what he and Kilburn were told by Newman in the 'few lectures' that he gave them in 1947. Yet in its detailed twists and turns, the story of the coming into existence of the Baby is much more complicated than Williams' summary conveys:
About the middle of the year [1946] the possibility of an appointment at Manchester University arose and I had a talk with Professor Newman who was already interested in the possibility of developing computers and had acquired a grant from the Royal Society of £30,000 for this purpose. Since he understood computers and I understood electronics the possibilities of fruitful collaboration were obvious. I remember Newman giving us a few lectures in which he outlined the organisation of a computer in terms of numbers being identified by the address of the house in which they were placed and in terms of numbers being transferred from this address, one at a time, to an accumulator where each entering number was added to what was already there. At any time the number in the accumulator could be transferred back to an assigned address in the store and the accumulator cleared for further use. The transfers were to be effected by a stored program in which a list of instructions was obeyed sequentially. Ordered progress through the list could be interrupted by a test instruction which examined the sign of the number in the accumulator. Thereafter operation started from a new point in the list of instructions. This was the first information I received about the organisation of computers. ... Our first computer [the Baby] was the simplest embodiment of these principles, with the sole difference that it used a subtracting rather than an adding accumulator.
The use of subtraction as the basic arithmetical operation was a clever idea that simplified the logical design of the Baby computer. In an interview Williams explained why subtraction was chosen:
The facilities we decided to provide were the absolute minimum. For example, the only arithmetic operation we were able to perform was subtraction, because you can do addition by means of subtraction because you can subtract something from nothing and get its negative, and then subtract its negative from what you want to add it to, and you get the sum — and you can't do the opposite of this, you can't do anything by addition other than addition. So we had the one basic arithmetic operation, subtraction, and the other important thing that we had was the facility to take one of two paths through the programme according to the sign of the number standing in the accumulator. This is the basic thing about computers that makes them universal. So in all we had about five possible instructions that the machine could obey.
The detailed design of the Baby was largely done by Kilburn. 'I designed the smallest computer which was a true computer (that is a stored program computer) which I could devise', Kilburn said. It was Kilburn, too, who contributed the idea of basing the design around the single arithmetical operation of subtraction; when asked (by Copeland) whose idea this was, Kilburn replied simply 'Mine!'.
Nevertheless, the fundamental architectural ideas embodied in the Baby were neither Kilburn's nor Williams'.
Turing's influence on Kilburn

Turing

Tom Kilburn posing in front of the 1998 rebuild of the Manchester Baby Photo © Carolyn Djanogly.
 The Pilot Model of Turing's ACE in 1952
The Pilot Model of Turing's ACE in 1952

Turing
Turing's early input to the developments at Manchester, hinted at by Williams in his above-quoted reference to Turing, was via the lectures on computer design that Turing and his assistant Wilkinson gave in London during the period December 1946 to February 1947 (the lecture notes are in Alan Turing's Automatic Computing Engine). The lectures were held between 2 p.m. and 5 p.m. on successive Thursday afternoons in a rather dingy underground room at the Headquarters of the Ministry of Supply, then housed in the Adelphi Hotel, Baker Street, London. The series of nine lectures covered Versions V, VI, and VII of Turing's design for the ACE. Representatives attended from various organisations that planned to use or build an electronic computer. Among the audience was Kilburn. Turing's lectures—which occurred several months before the lectures that Newman gave Williams and Kilburn at Manchester—played a key role in introducing Kilburn to the fundamentals of computer design.
Kilburn usually said, when asked where he got his basic knowledge of the computer from, that he could not remember; for example, in a 1992 interview he said, 'Between early 1945 and early 1947, in that period, somehow or other I knew what a digital computer was ... Where I got this knowledge from I've no idea'. However, in his first report on the Manchester computer work, dated 1947, Kilburn referred to 'unpublished work' by Turing—and used various of Turing's technical terms. (These included 'table of instructions' and 'universal machine', and also various terms that, whether or not they originated with Turing, were distinctive of Turing's 1946-7 lectures—for example, 'source', 'destination', 'temporary store', 'staticiser', and 'dynamiciser'.) In a subsequent report written when the computer was working, Kilburn said 'I wish to acknowledge my indebtedness to Prof. M. H. A. Newman, and Mr. A. M. Turing for much helpful discussion of the mathematical requirements of digital computing machines'. Williams summed up Turing's role in this way: Turing was 'instrumental, with Newman, in instructing us in the basic principles of computing machines, not on the engineering side of course, on the mathematical, and we had very close collaboration with both of them'.
Turing's influence on the evolution of Kilburn's design for the Baby machine was in fact considerable. In December 1947 Kilburn described a 'hypothetical' machine, in a report to TRE dated 1 December. The hypothetical machine, he said, had 'the sole purpose of demonstrating the function of the storage system'.In Kilburn's hypothetical machine, each of the machine's elementary arithmetical and logical operations is implemented by a separate hardware unit or 'destination'; each of these units is numbered and the numbers are referred to by Kilburn as 'destination numbers'. Each instruction, Kilburn explained, transferred a number 'from one part of the machine—a "source"—to another—a "destination"'. An instruction consisted of two numbers, a source number s and a destination number d, which control a source tree and a destination tree respectively. In Kilburn's design, as in Version V of the ACE, instructions contained no 'operation code' (an operation code is the code-name of a operation, for example addition). The operation that was to be performed was implied by the destination number. The source tree accesses the number with address s in the main memory, and the destination tree accesses the destination, which is to say accesses the unit that will perform the required operation, e.g. the adder. Each operand is routed from the main memory via the source tree to the destination tree. There was no central accumulator, and everything was very different from the centralised design being promulgated by von Neumann in the United States.
Concerning the provenance of his design, Kilburn said rather vaguely that the design 'contain[ed] the essential framework of proposed machines'. In fact, the 'decentralised' structure that he proposed is extremely similar to Turing's design for the ACE.In the ACE there was no central accumulator, but rather a collection of different destinations (delay lines) where the different operations were performed—addition, subtraction, test whether zero, and so forth. The explanation of how it was that by 1947 Kilburn 'somehow or other ... knew what a digital computer was' is no mystery: Turing taught him!
Here, in briefest outline, is the explanation that Kilburn received, during the 1946-7 lectures, of how to build a computer:
Transfer of numbers is achieved by indicating a SOURCE and a DESTINATION by the control system. ... Certain [delay] lines are used exclusively for certain purposes ... For example, lines 2 and 3 are always used for addition. ... In order that a combination of 10 signals ... may be used to tap any source or open any destination a system of inter-connection is arranged, which is known as a TREE. ... In Versions V and VI the Source and Destination trees control 1024 Sources and Destinations.
(For a complete description of the ACE's architecture and instruction formats see Alan Turing's Automatic Computing Engine, chapters 4, 9, 11 and 22.)
It is clear, then, that Turing supplied the central ideas leading to Kilburn's 1947 hypothetical machine: the basic design of the machine was that proposed by Turing for the ACE and described in Turing's 1946-7 lectures. In an interview Kilburn said dismissively that the 'only thing' he 'got from' Turing's lectures 'was an absolute certainty that my computer wasn't going to look like that'. He did not explain, though, that he came to this decision only by designing a detailed hypothetical machine in the Turing mould!
Turing was Kilburn's mentor, but once Kilburn had learned all he neede, he went his own way, and his 1947 ACE-like design was in fact a dead end; it bore very little relation to the actual Baby. The Baby was a centralised machine (see diagram). Three cathode ray tubes (marked 'S', 'A', and 'C' in the diagram) formed the Store, Accumulator, and Control. All calculations were performed by transfers of numbers between the Store and the central Accumulator.
Kilburn himself, in later life, was an important source of what has unfortunately become the canonical view of the roles of Turing and Newman—or rather their lack of role—in the origin of the Baby. Although in his first papers on the Manchester computer Kilburn gave credit to both Turing and Newman, in later years he was at pains to assert the independence of his and Williams' work from outside influence, presenting the history of the Baby in a way that assigned no role to Turing or to Newman. In an interview (with Copeland) in 1997, Kilburn emphasised that Newman 'contributed nothing to the first machine' (the Baby). Kilburn said: 'What I'm saying is that the origin is not Newman in any way whatsoever. I know it has been described by others as such—but it wasn't'. Turing's only contributions, Kilburn said, came after the computer was working, and included preparing a 'completely useless' programming manual.
Another claim in the orthodox history of computing is that the Manchester computer was a wholly and uniquely British achievement—the very first modern computer, conceived and built by Kilburn, Williams and a couple of lads, in the same city that had given birth to the first industrial revolution nearly two centuries previously. However, close study of the documentary evidence reveals the considerable extent to which the Baby was indebted to American ideas.

von Neumann

Jack Good, codebreaker and computer pioneer
12. The Manchester Computer and John von Neumann

The fog disperses at the Princeton Institute for Advanced Study.
Photo © Thomas Uphill.

The Baby

Members of the Princeton computer team. From left: John von Neumann, Julian Bigelow, James Pomerene, Herman Goldstine.

The Princeton IAS computer. 20 Williams Tubes in cannisters are visible; another 20 are on the opposite side of the machine.
The 1957 American Family Tree of Computer Design (right) depicted the Manchester development as a slim branch sprouting from the strapping EDVAC trunk. However, the Tree also mistakenly portrayed the ACE as an outgrowth from the same sturdy trunk. Those who drew the tree in the late 1950s were blissfully ignorant of Colossus, and failed to recognise the other trunk on the opposite side of the Atlantic. Yet in the case of the Manchester computer, by a mixture of luck and jingoism the authors of the tree got the picture partly right.
The key question is: to what extent was the design of the Manchester Baby influenced by the thinking of von Neumann and his associates at the Moore School and Princeton? (Presper Eckert's role has already been touched upon in the sub-section The regeneration principle. According to the Manchester engineers, the answer to this question is 'Not much, if at all'. Kilburn spoke scathingly of the von Neumann 'dictat' and Geoff Tootill said:
Williams, Kilburn and I (the three designers of the first Manchester machine) had all spent the 1939–1945 war at the Telecommunications Research Establishment doing R & D on radiolocation equipments. The main U.S. ideas that we accepted in return for our initiatives on these and later on computers were the terms 'radar' and 'memory' ... We disliked the latter term, incidentally, as encouraging the anthropomorphic concept of 'machines that think'.
To the best of my recollection FC [Williams], Tom [Kilburn] and I never discussed ... von Neumann's ... ideas during the development of the Small-Scale Experimental Machine [the Baby], nor did I have any knowledge of them when I designed the Ferranti Mk I. I don't think FC was influenced at all by von Neumann ... I think he was in general quite punctilious in acknowledging other people's ideas.
Williams himself, however, was aware that the thinking of the Manchester engineers might have been indirectly influenced by von Neumann. In a letter, after emphasising the fact that his first knowledge of computer design came from Newman, he remarked that the information 'may have derived from America through Newman'.
Newman, like Turing, was well aware of von Neumann's 'First Draft of a Report on the EDVAC', and Newman did not share Turing's predilection for working alone from his own first principles. Newman was eager for all the fresh ideas about computers he could gather. In the summer of 1946 he and Jack Good visited Turing at the National Physical Laboratory for several days, in order to learn as much as they could about the design of the ACE. Good was a leading cryptanalyst in the Newmanry and a co-designer of some of the equipment in Colossus II; in October 1945 Newman appointed him to the Manchester Mathematics Department. (Good tells his own story in his chapter 'From Hut 8 to the Newmanry' of Colossus: The Secrets of Bletchley Park's Codebreaking Computers.) Also in the summer of 1946 Newman sent David Rees, another ex-Newmanry mathematician with an interest in computers, to the Moore School lectures, where Eckert, Mauchly, and other members of the ENIAC–EDVAC group publicised their ideas on computer design. In the autumn of 1946 Newman himself went to Princeton for three months. Von Neumann's co-authored report 'Preliminary Discussion of the Logical Design of an Electronic Computing Instrument' (June 1946) was studied closely at Manchester, although not by the engineers.
On his return to Manchester from Princeton, Newman gave two or three lectures on computer design to Williams and Kilburn (described above). He covered the Princeton plans together with ideas of his own. Turing's lecture series had already provided Kilburn with a detailed and extended introduction to the state of the art; but Newman's emphasis on the use of a central accumulator must have opened Kilburn's eyes to the simplicity of a centralised design.
Newman's lectures inspired Good to write a few pages of notes expressing his first ideas on what the basic operations of a general-purpose computer should be. These notes, which share notation with von Neumann's 'Preliminary Discussion' (e.g. 'CC' for conditional transfer of control, 'l' and 'r' for left and right shift, and 'R→A' for the operation of transferring the number in the accumulator A to the arithmetic register R), are a glorious mixture of ideas originating from Princeton, Newman, and Good himself.
In 1998, in his acceptance speech for the IEEE Computer Pioneer Award, Good announced that he had made a proposal for the Baby machine's basic instructions; the proposal was made 'at Kilburn's request', he said. In May 1947 Good prepared an eight-page document for Kilburn, titled 'The Baby Machine'; this was written, he said, in response to a call from Kilburn 'for suggestions for a small number of basic instructions (or operations)'.The 12 basic operations listed by Good were: (1) transfer the number in 'house' x (there were 64 'houses' or storage registers) to the accumulator A; (2) add the number in house x to the number in the accumulator and store the result in the accumulator; (3) transfer the negative of the number in house x to the accumulator; (4) subtract the number in house x from the number in the accumulator and store the result in the accumulator; (5) transfer the number in the accumulator to (arithmetic) register R; (6) transfer the number in R to the accumulator; (7) transfer the number in the accumulator to house x; (8) transfer the number in house x to R; (9) shift the number in the accumulator one place to the left; (10) shift the number in the accumulator one place to the right; (11) transfer control unconditionally to the instruction in house x; and (12) conditional transfer of control, viz transfer control to the instruction in house x if the number in the accumulator is greater than or equal to 0. Good then gave some examples of programs for this baby machine, including multiplication of arbitrary numbers (between -231 and 231) and testing the parity of a number.
The set of basic operations that Good supplied to Kilburn was in fact nothing more than a simplification of the more complex set given in von Neumann's 'Preliminary Discussion of the Logical Design of an Electronic Computing Instrument'. Von Neumann had himself pointed out that the set of operations he listed could be simplified, saying 'many can be programmed by means of the others'. (Of Good's 12 operations, only number (5)—transfer the number in A to R—was not in von Neumann's larger set.) Good had injected Princeton ideas into Kilburn's thinking.
Kilburn's instruction set for the 1948 Baby was a subset of Good's May 1947 instruction set. Kilburn reduced Good's set of 12 elementary operations to 5: (3), (4), (7), (11), a modified form of conditional transfer of control (skip the next instruction in the store if the number in the accumulator is less than 0), and a sixth operation, stop the machine. Good's operations (1) and (2) were unnecessary for Kilburn's purposes, since subtraction was to be his only basic arithmetical operation. The two shift operations (9) and (10) were logically redundant, and could be dispensed with in a minimal machine (as Good noted, the left shift is just multiplication by 2, and the right shift is division by 2). Good's instructions (5), (6) and (8) were also unnecessary, since there was no arithmetic register R in the Baby.
Once Kilburn had had the idea that the only arithmetical operation should be subtraction, and had reduced Good's instruction set from 12 basic operations to 5, he knew what he needed to build: a minimal machine whose hardware components were the Store, Accumulator, and Control presupposed by Good's operations.
Kilburn never acknowledged a debt to Good—let alone to von Neumann—but as he himself said, 'You can't start building until you have got an instruction code'. Talking about the origin of the basic instructions in an interview with Copeland, Kilburn said that 'these instructions sort of write themselves'. He did not mention Good.As to von Neumann, Kilburn listed 'Unpublished work, von Neumann, J.' among the references for his December 1947 report to TRE. However Kilburn, and the other engineers working on the Baby, were almost certainly unaware of the true extent of their indebtedness to von Neumann. Kilburn did not realise that Good was in effect acting as a courier, carrying Princeton ideas to himself and Williams—or that Newman had played a similar role in his 1947 lectures. The logical design of the 1948 Baby is in fact virtually identical to a 1946 Princeton design by von Neumann and his group—a finding that places the Manchester Baby in a very new light.
From the beginning Newman's plan had been that, in order to have a computer ready for experimental work as soon as possible, 'one of the types already under construction in 1946 should be copied'. Huskey, who paid a visit early in 1947 to the Newman–Williams project (as he called it) said in his write-up of the visit: 'They are planning to more or less copy the von Neumann scheme'.Despite Kilburn's flirtation with a Turingesque design later in 1947, the 1948 Baby was a very close relative indeed of the (more complex) machine described in von Neumann's 'Preliminary Discussion of the Logical Design of an Electronic Computing Instrument'. Both were single-address machines with a central accumulator. Moreover the control arrangements for the two machines were virtually identical. Simplifications were achieved in the Baby by (i) using much less memory than von Neumann specified, (ii) using fewer basic operations, (iii) using a more restricted form of conditional transfer of control (see above), (iv) storing only one instruction per word, rather than two as in the Princeton design, and (v) opting for a serial design. The Princeton design involved 40 memory units working in parallel. (Kilburn's view on parallelism? 'Given unlimited money, quite right!')

Harry Huskey examining one of the SWAC's 40 Williams Tubes
Huskey's 1947 summary of logical aspects of the Princeton design (published in Alan Turing's Automatic Computing Engine) makes it obvious that the design of the Baby adhered very closely to American thinking. Aside from Kilburn's idea of using subtraction as the single basic arithmetical operation, the basic logical structure of the Baby was more or less identical to that being proposed at Princeton. Huskey wrote in 1947:
Princeton. In the von Neumann plan the machine consists essentially of a memory and a static accumulator. All transfers from the memory to the accumulator are essentially additions. The orders used are of the following type:
| (1) |
Clear A |
This clears the accumulator. |
| (2) |
x to A |
Adds the number in position x in the memory to the contents of the accumulator. |
| (3) |
A to x |
Transfers the number in the accumulator to position x of the memory. |
| (4) |
C to x |
Transfers control to x; i.e., the next order to be obeyed is in position x in the memory. |
| (5) |
CC to x |
Conditional transfer of control; i.e., control is transferred to x in the memory if the number in A is negative. Otherwise, control obeys consecutive orders in the memory. |
The Baby's originality certainly does not lie in its logical design, but in its cathode ray tube memory and its electronic engineering. It was as electronic engineers, not computer architects, that Williams and Kilburn led the world in 1948.

Kilburn standing at the console of the Ferranti Mark I computer at Manchester University. Seated are Ferranti engineers Keith Lonsdale (left) and Brian Pollard.
Just as key logical ideas flowed from Princeton to Manchester, key engineering ideas flowed in the opposite direction. A pre-publication version of the Williams–Kilburn report 'A Storage System for Use with Binary Digital Computing Machines' was read eagerly at Princeton in June 1948. As soon as von Neumann's chief engineer Julian Bigelow read about the Williams Tube he 'realized at once that it could be used exactly as we wished' (wrote von Neumann's collaborator Herman Goldstine). Since 1946 von Neumann's plan had been to use the RCA Selectron memory tube, under development elsewhere in Princeton, but by 1948 this was still nowhere close to working. In the summer of 1948 Bigelow travelled to Manchester to see the Williams Tube memory in operation. He was impressed by what he described as Williams' 'inventive genius'.
When the Princeton computer was eventually completed in 1951, its main memory consisted of 40 Williams Tubes. The Williams Tube, said Goldstine, made 'a whole generation of electronic computers possible'. Another Manchester invention to travel to Princeton (although not in time to be incorporated in the Princeton computer) was the index register, or 'B-tube', for which Kilburn, Newman, Tootill and Williams shared the patent. Goldstine described the index register as a 'very significant modification instituted by Kilburn of the Manchester group' (although Kilburn's name did not come first on the patent). Index registers, which enable instructions to be modified while the program is running, are now a standard part of computer technology.

Turing standing at the console of the Ferranti Mark I computer at Manchester University. Here Turing pioneered the field of research now called Artificial Life.
13. Turing Joins the Manchester Project
In May 1948 Turing resigned from the NPL. Work on the ACE had drawn almost to a standstill (see chapter 20 Third Attempt to Build the ACE: the Disastrous Thomas Era and chapter 21 Turing Leaves the NPL). Newman lured a 'very fed up' Turing to Manchester, where he was appointed Deputy Director of the Computing Machine Laboratory (there was no Director).
Once Turing arrived in Manchester he got the computer working properly, designing an input mechanism and the programming system for an expanded machine, and he wrote a programming manual. The first of the production models, marketed by Ferranti, was completed in February 1951 and was the first commercially available electronic digital computer. The first U.S. commercial machine, the Eckert–Mauchly UNIVAC, was delivered a few weeks later in March 1951.
In a letter Williams described what was, from his point of view as an engineer, Turing's 'major contribution' to the full-scale machine:
Our first machine had no input mechanism except for a technique for inserting single digits into the store at chosen places. It had no output mechanism, the answer was read directly from the cathode ray tube monitoring the store. At this point Turing made his, from my point of view, major contribution. He specified simple minimum input facilities from five hole paper tape and output from the machine in similar form.
This five-hole paper tape was the daily bread of Bletchley's attack on Tunny. So too was the five-bit teleprinter code which Turing used at Manchester to express machine-code programs in the form of keyboard characters.
Elsewhere Williams provided some additional detail. Turing explained to the engineers
how you could organise a paper tape input machine to load a computer. ... [Turing] was of immense value to us in telling us precisely what signals he would need to operate his tape input machine, precisely what signals he would need to operate his tape punch.
This input machine employed a row of photocells to read the moving teleprinter tape—technology similar to that used in Colossus and Heath Robinson. The device delivered input to the Manchester computer at the rate of 200 five-bit characters per second, which approached the maximum that the computer was able to handle. This represented only 4% of the normal input rate of Colossus I, however!
Turing and Newman also contributed to the instruction set of the full-scale computer. Tootill said:
As well as our own ideas, we incorporated functions suggested by Turing and Newman in the improvement and extension of the first machine. When I did the logic design of the Ferranti Mark 1, I got them to approve the list of functions.
Kilburn reported that at this time (1949) Newman contributed another key idea to the plans for the full-scale computer: the concept of multilength numbers. Newman proposed that a facility be included in the machine for linking together arbitrary numbers of words of memory, so that arithmetical operations could be carried out on numbers of various lengths. This idea was present in Version V of Turing's ACE design (1946).

The EDSAC, built by Maurice Wilkes at the University of Cambridge

Harry Huskey at the console of the SWAC (National Bureau of Standards Western Automatic Computer)
At Manchester Turing at last had his hands on a stored-program computer. He was soon using Manchester University's Ferranti Mark I to model biological growth (see chapter 10 Turing and Artificial Life). And while the rest of the world was just waking up to the idea that electronics was the new way to do binary arithmetic, Turing was talking very seriously about programming digital computers to think (see chapter 9 Turing and Artificial Intelligence).
14. Other Early Stored Program Computers
The EDSAC, built by Maurice Wilkes at the University of Cambridge
Mathematical Laboratory, was the second electronic stored-program
computer to run, in May 1949. (It was at
a conference held in June 1949 to celebrate the inauguration of the
EDSAC that Turing presented his early paper on what is now called
program verification, 'Checking a Large Routine'.)
Later in 1949 came: the BINAC, built by the creators of the ENIAC,
Eckert and Mauchly, at their Electronic Control Company, Philadelphia
(opinions differ as to whether the BINAC ever actually worked); the CSIR Mark 1, built by Trevor Pearcey at the
Commonwealth Scientific and Industrial Research Organisation Division
of Radiophysics, Sydney, Australia; and Whirlwind I, built by Jay
Forrester at the Digital Computer Laboratory, Massachusetts Institute
of Technology.
The SEAC, built by Samuel Alexander and Ralph Slutz at the U.S.
Bureau of Standards in Washington D.C., first ran in April 1950; and
the SWAC, built by Harry Huskey at the Institute for Numerical
Analysis on the campus of the University of California at Los
Angeles, in August 1950.
While the EDVAC itself was not fully working until 1952, most of the
computers just mentioned were influenced by the EDVAC design.

Turing
15. Womersley Recruits Turing to the National Physical Laboratory

The name 'Automatic Computing Engine' was due to Womersley, the administrative head of the ACE project, and the story of the ACE begins with his appointment as
Superintendent of the newly created Mathematics Division of the
National Physical Laboratory. Womersley's proposed research programme for his new Division included
the items 'To explore the application of switching methods
(mechanical, electrical and electronic) to computations of all
kinds', 'Investigation of the possible adaptation of automatic
telephone equipment to scientific computing', and 'Development of
electronic counting device suitable for rapid computing'.
Womersley had himself been a member of the Interdepartmental
Technical Committee that in April 1944 had recommended the creation
at the NPL of a Mathematics Division whose primary objective was to
'undertake research into new computing methods and machines'. In its report the Committee emphasized that the new division should
be provided with 'facilities for designing new machines and perhaps
for constructing pioneer ones', noting 'it is probable that new
machines may be called for of patterns that cannot be foreseen now'.
In December 1944 Womersley addressed the Executive Committee of the
NPL on the potential of electronic computing. His proposals were
far-sighted at a time when no electronic computers were in existence
apart from the—invisible—Colossus. The minutes of the
meeting summarize his speech:
Electronic counting devices ...
can be used and machines can be constructed which have a high degree
of flexibility and which can be continually improved and extended.
Electronic counting can be done at the rate of one operation per
microsecond, a vast improvement on anything previously attempted. All
the processes of arithmetic can be performed and by suitable
inter-connections operated by uniselectors a machine can be made to
perform certain cycles of operations mechanically... . [T]here is no reason why the instructions to the machine should not
depend on the result of previous operations so that various iterative
types of method could become fully automatic.
In November 1946 Womersley wrote a fascinating synopsis of the principal events
that led to the establishment of the ACE project:

Howard Aiken and the Automatic Sequence-Controlled Calculator

George Stibitz at Bell Labs
1936-37 Publication of paper by A. M.
Turing 'On Computable Numbers, with an Application to the
Entscheidungsproblem'... .
1937-38 Paper seen by J.R.W. [J.R.
Womersley] and read. J.R.W. met C.L. Norfolk, a telephone engineer
who had specialised in totalisator design and discussed with him the
planning of a 'Turing machine' using automatic telephone equipment.
Rough schematics prepared, and possibility of submitting a proposal
to N.P.L. discussed. It was decided that machine would be too slow to
be effective.
June 1938 J.R.W. purchased a uniselector
and some relays on Petty Cash at R.D. Woolwich for spare-time
experiments. Experiments abandoned owing to pressure of work on
ballistics... .
1942 Aiken's machine [the
Sequence-Controlled Calculator at Harvard University] completed and
working.
1943 Stibitz constructed the Relay
Computor at Bell Telephone Laboratories.
Late 1943 J.R.W. first heard of these
American machines.
1944 Interdepartmental Committee on a
Central Mathematical Station. D.R. Hartree mentioned at one meeting
the possible use of automatic telephone equipment in the design of
large calculating machines. J.R.W. submitted suggestions for a
research programme to be included in Committee's Report.
1944 Sept. J.R.W. chosen for Maths.
Division.
1944 Oct. J.R.W. prepares research
programme for Maths. Division which includes an item covering the
A.C.E.
1944 Nov. J.R.W. addresses Executive
Committee of N.P.L. Quotation from M/S (delivered verbatim) ...
'Are we to have a mixed team developing gadgets
of many kinds ... Or are
we, following Comrie ...
to rely on sheer virtuosity in the handling of the ordinary types of
calculating machines? I think either attitude would be disastrous ...
We can gain the advantages of both methods by adopting electronic
counting and by making the instructions to the machine automatic ...
'
1945 Feb-May J.R.W. sent to the U.S.A. by
Director. Sees Harvard machine and calls it 'Turing in hardware'.
(Can be confirmed by reference to letters to wife during visit).
J.R.W. sees ENIAC and is given information about EDVAC by Von Neumann
and Goldstine.

It has not been possible to locate a photograph of Womersley. The background shows the inside of the Babbage Building, part of Womersley's Mathematics Division.
1945 June J.R.W. meets Professor M.H.A.
Newman. Tells Newman he wishes to meet Turing. Meets Turing same day
and invites him home. J.R.W. shows Turing the first report on the
EDVAC and persuades him to join N.P.L. staff, arranges interview and
convinces Director and Secretary.
Persuading Turing to join the embryonic ACE project was a great coup,
testifying to Womersley's vision and initiative (even locating
Turing, who was at that time engaged in secret work, could not have
been straightforward). Turing was even more highly qualified for the
job than Womersley realised. While Womersley clearly understood the
importance of Turing's pre-war article 'On Computable Numbers, with
an Application to the Entscheidungsproblem', he was completely
unaware of the highly secret developments in electronic computing
that had taken place during the war at Bletchley Park, where Turing was among the few who knew of Colossus.
16. Turing's Design Document 'Proposed Electronic Calculator'
Turing's employment at the NPL commenced on 1 October 1945, by which time
Mathematics Division was 'functioning on a limited scale'. Turing set to work on the design of the Automatic Computing Engine.
By the end of 1945 he had completed his technical report 'Proposed
Electronic Calculator'. Womersley's next step was to present Turing's design to the Director of the
NPL, Darwin, in order to secure the support necessary for the
project. He wrote to Darwin:

The Daily Telegraph, 7 November 1946
“ACE” Machine Project.
With this minute I present three reports. The
first is a short account, by Hartree and myself, of recent
developments in the U.S.A. in the field of automatically controlled
calculating machines. The second is a report by Dr. A. M. Turing which
shows how such a machine could be constructed (by combining
electrical apparatus already well-developed and having known
properties) which would be capable of solving a wide variety of
problems at speeds hitherto unattainable.
It is very important to mention that this device
is not a calculating machine in the ordinary sense of the word. One
does not need to limit its functions to arithmetic. It is just as
much at home in algebra, i.e. it can work out matrix multiplications
in which the elements are algebraic polynomials, or problems in
Boolean Algebra, or the enumeration of group characters. Methods of
successive approximation, i.e. the Southwell “Relaxation”
process, are equally possible, since the machine will contain a
device which enables it to choose between two sets of instructions
according to the sign of some number in it.
The cost is, naturally, a doubtful point. I put
it, after careful consideration, at £60,000 - £70,000,
though it is difficult to be sure of a “ceiling”. It
will, I believe, be one of the best bargains the D.S.I.R. [Department
of Scientific and Industrial Research] has ever made. To give some
idea of the speed of the machine, it will calculate a gun trajectory,
from muzzle to point of fall, in less than 30 seconds, and it would
carry through the preparation of the whole of the ballistic bombing
tables for the R.A.F. in a few weeks, apart from printing. By its use
we can explore whole fields of both pure and applied mathematics at
present closed to us by the formidable magnitude of the computing
programmes involved.
We can attack complicated integral equations,
integro-differential equations and partial differential equations by
replacing them by large blocks of simultaneous linear equations in
700-1000 unknowns and solve them with ease and speed. We can take T.
Smith's theory of the design of optical instruments and use it on
practical design problems at a speed which will enable answers to be
given to the firms by telephone in a few hours. We can revolutionise
the study of compressible fluid flow, and of aircraft stability.
Problems now slowly attacked piecemeal will be capable of solution as
a whole. The machine will also grapple successfully with problems of
heat-flow in non-uniform substances, or substances in which heat is
being continuously generated. It will enable the study of materials
with peculiar elastic properties (e.g. plastics) to be advanced in a
way that is impossible with present computing resources... . [W]e could alter the whole tempo of the numerical mathematical work
associated with the scientific research of this country if the
machine were available.
The possibilities inherent in this equipment are
so tremendous that it is difficult to state a practical case to those
who are not au fait with the American developments without it
sounding completely fantastic. But if anyone is going to suggest that
this equipment is expensive, may I point out that two machines in the
U.S.A., the Harvard Sequence Controlled Calculator, and the Bell
Telephone Laboratory Relay Computer, cost as much an this, work at
1/1000th the speed, will have neither the versatility nor the storage
capacity, and yet were thought by the Americans to be worth while.
The third document is an attempt to state a
practical case for the equipment. In view of the unique nature of the
equipment this is difficult, but I believe that in this direction the
promised support of Commander Sir Edward Travis, of the Foreign
Office, will be invaluable....
As regards the manufacture of the machine, I
think that the Post Office Engineering Research Station is the right
place, if they can see their way to do it. Mr. Flowers, of that
Station, has had wartime experience in the right field, and, during
his recent visit to the U.S.A., visited the places where these
developments have been going on.
Approval for the ACE project rested with the Executive Committee of
the NPL and Womersley duly prepared a paper for presentation to the
Committee:
Memorandum by Mr. J. R. Womersley,
Superintendent,
Mathematics Division
The research programme of the Mathematics
Division contains an item “To explore the application of
switching methods (mechanical, electrical and electronic) to
computations of all kinds.” ...
Dr. A. M. Turing was appointed to the staff of the Division, and
began to consider the possibilities of electronic methods ...
Dr. Turing has now completed a long report, which makes definite
proposals for the construction of a machine, capable of solving a
wide variety of problems at speeds hitherto unattainable... .
Summary of Part I of Dr. Turing's Report
It is intended that the ACE machine shall tackle
whole problems, i.e. that instead of repeatedly using human labour
for taking material out of the machine and putting it back at the
appropriate moment, all this will be done by the machine itself. It
will not be limited to carrying out a sequence of prescribed
operations. Provision is made for making the behaviour of the machine
to depend on the results of its own calculations.
Once the human element is eliminated, the
increase in speed is enormous. For example, it is intended that the
multiplication of two ten-figure numbers shall be carried out in 500
microseconds, about 20,000 times the speed of a normal calculating
machine. This speed is not attained by making the equipment more
expensive and more elaborate than it need be. It is the natural
result of the unconventional methods used, and once this is granted,
there is no economy to be obtained by reducing it.

Mercury delay lines

Instructions in a delay line, viewed on a monitor
The basic principle is that numbers contained in
the machine are stored dynamically, not statically as in other
machines. The internal working of the machine is entirely in the
binary system, and a number is represented by a series of 1's and
0's, the 1's being pulses, and the 0's the spaces between them. The
digit of least significance comes first in point of time. The
problem is to find a way of storing a number in this form, so that it
can be kept circulating in the machine until it is needed again for
use in a subsequent calculation. Dr. Turing describes a 'delay line,'
the 'circulating memory' used in radar, which he shows to be suitable
for this purpose. The manufacture of memories capable of
accommodating 1000 binary digits is shown to be practicable.
The machine then divides into two main parts, an
arithmetical organ, and a logical control, with input and output
organs for communication with the outside world. The instructions to
the machine can themselves be expressed in the form of numbers in the
binary scale, and fed into the logical control part of the machine at
the beginning of a problem. There they circulate in the appropriate
delay lines until the numerical information (“initial
conditions”) has been fed in, the final information being
another instruction, the “instruction to proceed.”
...
The original intention was that each unit would consist of 32 binary
digits, the first digit being '0' or '1' according to the nature of
the 'number' i.e. whether it is a number or an instruction, the
second being an indication of sign. Dr. Turing has extended this
idea to make it more flexible. Each 'number' consists of two units of 32 binary digits. One of these contains a number in the
binary system between zero and unity, the other gives its
'significance,' i.e. a power of 2 by which it must be multiplied, its
sign, and some spare digits which are used to identify the number.
The processes of arithmetic are very simple. To
add two numbers they are taken out of storage and by passing them
through a simple network of radio valves, they are 'glued' together
and the sum deposited in another storage element.
Multiplication is done by repetitions of this
process, with appropriate time delays. It is proposed to do division
by multiplication by the reciprocal, the reciprocal being calculated
by successive approximation. This is quite practicable in view of the
high speed of the unit processes.
The scope of the machine is very wide. It is
envisaged that the construction of a set of range tables could be
treated as a single problem, and that once experience is gained,
could be run off in a few days. As an indication of speed, it should
be possible to calculate a gun trajectory by 'small arcs' from muzzle
to point of fall, in about half a minute. All types of 'relaxation'
calculation can be fully mechanised - indeed all methods of
successive approximation. Matrices of degree less than 30 whose
elements are polynomials of the tenth degree can be multiplied,
giving another matrix with polynomial coefficients. Other examples
are given in the report. Some attention is also given to the problem
of checking, since the machine must inspire confidence in its
results. This cannot be dealt with adequately until actual
manufacture begins... .
The cost of the proposed machine will be about
the same as the ENIAC constructed for the Aberdeen Proving Ground,
and somewhat less than the Bell Telephone Relay Computer. The cost of
the Harvard University machine is not known with accuracy, but is
reputed to be half-a-million dollars. If it is granted that this
country should possess one of these large machines, the Mathematics
Division of the N.P.L. is the obvious place for it. The machine
envisaged by Dr. Turing would have an output equal to the total
output of all the large machines so far constructed in the U.S.A. In
fact we are now in a position to reap handsome benefits from the
pioneer work done in the United States, and it is undoubtedly
advisable that we should build this type of machine at once, rather
than begin with relay equipment.

Colossus VII
As mentioned previously, Womersley had
no knowledge of Colossus. Consequently his view of the technological developments in
computing was distorted, and he tended to exaggerate the intellectual
debt owed by the ACE to the ENIAC and to the relay (i.e.
non-electronic) machines at Harvard and Bell Labs.
Womersley's Memorandum and Turing's
'Proposed Electronic Calculator' were submitted to the Executive
Committee of the NPL in February 1946. Discussion was deferred until
the March meeting, when the 'Committee resolved unanimously to
support with enthusiasm the proposal that Mathematics Division should
undertake the development and construction of an automatic computing
engine of the type proposed by Dr. A. M. Turing'. The minutes of the meeting recorded Womersley's opening remarks,
Turing's short lecture, and the ensuing discussion:
Large Electronic Calculating Machine ACE
The Committee had before it Paper E.881
(Memorandum by Mr. J. R. Womersley, Superintendent, Mathematics
Division, concerning the “ACE” Machine Project) and Paper
E.882 (Report by Dr. A. M. Turing On Proposals for the Development of
an Automatic Computing Engine (ACE)).
The Chairman invited Mr. Womersley to outline
the reasons why a machine of the type proposed by Dr. Turing should
be constructed for the Mathematics Division.
Mr. Womersley said that he believed it possible
to see these proposals in their true perspective if one had knowledge
of what had been done in the U.S.A. during the war. He therefore
proposed to begin by sketching in some of the background of recent
developments.
Mr. Womersley then gave a brief description of
three large calculating devices constructed in the U.S.A. during the
war - the I.B.M. Sequence Controlled Calculator at Harvard
University, the Relay Computer designed by Dr. G. R. Stibitz of
Bell's Telephone Laboratories, and the ENIAC, constructed at the
Moore School of Electrical Engineering, University of Pennsylvania
for the Ballistics Research Laboratories, Aberdeen Proving Ground.
Each one of these machines had cost from £80,000-£100,000.
It was interesting to note that Dr. Turing's machine, when fully
completed, would have a potential output of work greater than the
three of them put together. In other words, we now had the
opportunity to begin work in this field at a most favourable moment.
The machine proposed had not only a greater output, but greater
versatility than the machines so far made, because of the greater
elaboration of the logical controls proposed by Dr. Turing. This was
possible by reason of the different mode of operation, and the fact
that in Dr. Turing we had available an expert in the field of
mathematical logic.

Turing
Mr. Womersley then introduced Dr. A. M. Turing,
who was invited to describe the principles underlying his proposal.
Dr. Turing explained that if a high overall
computing speed was to be obtained it was necessary to do all
operations automatically. It was not sufficient to do the
arithmetical operations at electronic speeds: provision must also be
made for the transfer of data (numbers, etc.) from place to place.
This led to two further requirements - 'storage' or 'memory' for the
numbers not immediately in use, and means for instructing the machine
to do the right operations in the right order. There were then four
problems, two of which were engineering problems and two mathematical
or combinatory.
Problem (1) (Engineering). To provide a
suitable storage system.
Problem (2) (Engineering). To provide
high speed electronic switching units.
Problem (3) (Mathematical). To design
circuits for the ACE, building these circuits up from the storage and
switching units described under Problems 1 and 2.
Problem (4) (Mathematical). To break down
the computing jobs which are to be done on the ACE into the
elementary processes which the ACE is designed to carry out (as
determined in the solution of Problem 3). To devise tables of
instructions which translate the jobs into a form which is understood
by the machine.
Taking these four problems in order, Dr. Turing
said that a storage system must be both economical and accessible. Teleprinter tape provided an example of a highly
economical but inaccessible system. It was possible to store about
ten million binary digits at a cost of £1, but one might spend
minutes in unrolling tape to find a single figure. Trigger circuits
['flip-flops'] incorporating
radio valves on the other hand provided an example of a highly
accessible but highly uneconomical form of storage; the value of any
desired figure could be obtained within a microsecond or less, but
only one or two digits could be stored for £1. A compromise was
required; one suitable system was the 'acoustic delay line' which
provided storage for 1000 binary digits at a cost of a few pounds,
and any required information could be made available within a
millisecond. Dr. Turing explained the principle of the delay line,
which involved transmitting compression waves down a tube of liquid,
using piezo crystals both as transmitters and receivers of sound. The
output of the receiving crystal was amplified, restored to its ideal
shape and fed back to the transmitter. On account of the shape
restoring process it was possible for a signal to travel down the
tube many millions of times and remain recognisable.
Dr. Turing then gave a brief account of the high
speed switching problems involved in the ACE (Problems (2) and (3)).
Numbers were to be represented in the binary scale and valves were
only to be used as 'on-off' devices. Although switching units had not
yet been made there was every hope of success because the limiting
factors were electron transit time, and the allied quantity Oag/gm,
and the frequencies at which these became serious were well above
those at which the ACE would be operated (viz. about 1 Mc/s).
Switching circuit design (Problem (3)) was illustrated by means of
the adder circuit.
Time did not permit of an adequate account of
Problem (4).
In reply to a question from Professor Tyndall,
Dr. Turing explained that an elaborate system of checks would be
incorporated, so that the failure of any part would be immediately
indicated. It was not possible entirely to guard against the failure
of the checking system itself, but the probability of an undetected
error could be reduced to very small proportions. The majority of the
checks would be introduced through instruction tables and would
therefore require no special equipment.
The Director asked what would happen if the
machine were instructed to sum a series which actually diverged
although thought to converge. Dr. Turing replied that it was left to
the discretion of the man who constructed the instruction tables (the
controller) to state what the machine should do in these cases. The
summation could be specified to a given number of terms regardless of
convergence, or until the last term was less than a given amount;
preferably the controller should have worked out the theory of the
convergence to some extent so as to be able to incorporate a suitable
test. The Director asked what would happen in cases where the machine
was instructed to solve an equation with several roots. Dr. Turing
replied that the controller would have to take all these
possibilities into account, so that the construction of instruction
tables might be a somewhat “finicky” business.
Professor Hartree pointed out that the serial
operation of the machine makes it very economical in its use of radio
valves. It requires only 2000 valves as against 18000 in the ENIAC,
and gives a “memory” capacity of 6000 numbers compared
with the 20 numbers of the ENIAC. This greater capacity (and the
higher speed) are attained at no greater cost than the ENIAC. The
greater storage capacity is facilitated by the high speed, and this
is an important factor in gaining the economy in equipment.
Professor Hartree also pointed out that if the
ACE is not developed in this country the U.S.A. will sweep the field,
and reminded the Committee that this country has shown much greater
flexibility than the Americans in the use of mathematical hardware.
He urged that the machine should have every priority over the
existing proposal for the construction of a large differential
analyser.
Director enquired whether the machine could be
used for other purposes if it did not fulfil completely Dr. Turing's
hopes. Dr. Turing replied that this would depend largely on what part
of the machine failed to operate, but that in general he felt that
many purposes could be served by it.
There was next some discussion as to the
possible cost of the machine and Mr. Womersley said that a pilot
set-up could possibly be built for approximately £10,000, and
it was generally agreed that no close estimate of the overall cost of
the full machine could be made at this stage. As regards financing
the project, the Secretary stated that the initiation of the work
could be undertaken within the terms of the existing research
programme of Mathematics Division and that it was probable that
sufficient financial provision had been made for possible expenditure
during the 1946-7 financial year. It appeared desirable, however,
that the possible magnitude of the project should be understood by
Headquarters and the Treasury so that, as far as possible, assurance
could be obtained that work on the machine could be continued in
succeeding years in so far as financial provisions are concerned.

Newspaper cartoon of Wilkinson (Turing's assistant at the NPL from 1946) in 1952
Professor Hartree said that such a machine would
be a means for tackling completely new ranges of problems, and Dr.
Southwell reported that Professor G. I. Taylor had expressed the
opinion that the machine would be more useful than ENIAC. He hoped,
however, that when the machine was constructed, charges made for its
use would not be so high as to discourage its use by Universities,
etc. He felt that there should be no attempt at amortisation of the
cost of the machine, which might well run into £100,000, but
that this should be regarded as a contribution of the Laboratory to
the general good of the country.
The Committee resolved unanimously to support
with enthusiasm the proposal that Mathematics Division should
undertake the development and construction of an automatic computing
engine of the type proposed by Dr. A. M. Turing and Director agreed
to discuss the financial and other aspects of the matter with
Headquarters.

Cartoon of Wilkinson
In a letter, Dr. E. T. Paris expressed the
interest of Ministry of Supply in the development of such a machine,
and stated that he had consulted Colonel Phillips, Superintendent of
Applied Ballistics, and Dr. McColl, Superintendent of Theoretical
Research in Armaments, who foresaw that from their point of view the
main use of the machine would be for - (a) The calculations of
trajectories for all types of projectiles (shell, bombs, rockets and
guided missiles); (b) Internal ballistic calculations (the motion of
projectiles down the bore); (c) The solution of partial differential
equations by relaxation and characteristic methods. Dr. Paris also
enquired how soon the machine was likely to be a working concern and
to what extent it was likely to be available for use by his Ministry,
adding that if the project goes well, at a later date it would be
possible to consider whether it would be advisable to have a machine
of the same general type made for armaments research and allied work.
In reply to a question by Dr. Carroll, Mr.
Womersley said that as a very rough estimate he thought the cost of
duplicating the machine would be approximately 25 per cent of the
original cost, although the capacity of the machine would be such
that duplicates would not be needed. He pointed out, however, that
when such a machine is in use in his Division it will require the
employment of a higher proportion of senior officers in the
scientific class, because the machine itself will do much of the work
of the lower staff classes.
In April 1946 Darwin wrote as promised to 'Headquarters', the Department
of Scientific and Industrial Research (DSIR). Notice his claim,
mentioned earlier, that a single electronic computer might suffice
for 'the whole country':

Cartoon of Wilkinson
Automatic Computing Engine (ACE)
This is a proposal to construct a computing
machine of very much greater potentialities than anything done
hitherto, though a similar project is being worked out at present in
America. The proposal has already been foreshadowed in the research
programme of Mathematics Division, Item 6502 “To explore the
application of switching methods (mechanical, electrical and
electronic) to computations of all kinds.” In the past the
processes of computation ran in three stages, the mathematician, the
computer [i.e. the human computer], the machine. The mathematician set the problem and laid down detailed
instructions which might be so exact that the computer could do his
work completely without any understanding of the real nature of the
problem; the computer would then use the arithmetical machine to
perform his operations of addition, multiplication, etc. In recent
times, especially with use of punched card machines, it has been
possible gradually for the machine to encroach on the computer's
field, but all these processes have been essentially controlled by
the rate at which a man can work.

Cartoon of Wilkinson and the Pilot Model ACE in 1952
The possibility of the new machine started from
a paper by Dr. A. M. Turing some years ago, when he showed what a
wide range of mathematical problems could be solved, in idea at any
rate, by laying down the rules and leaving a machine to do the rest.
Dr. Turing is now on the staff of N.P.L., and is responsible for the
theoretical side of the present project, and also for the design of
many of the more practical details. The principles he enunciated have
now become practicable since it is possible to use electronics in the
machine so that its rate of operation is about a hundred thousand
times as fast as a man's. The proposed machine is primarily a system
of electronic circuits some of which do the arithmetic, while others
give the instructions in a codified form, also as numbers. But there
is another feature necessary in computation, which may be called the
memory; this corresponds to the fact that the human computer has at
intervals to turn back to the results of some previous calculation
and bring them forward again. In many ways the memory is the most
serious problem in the machine, but a variety of methods have been
proposed and some instruments have been made, and the choice among
them is largely a matter of economy, since there will need to be
several hundred organs of this type. At present it appears that the
best solution may be one developed for use in radar, which consists
in sending a stream of ultra-sonic pulses down a tube of liquid.
These are known as delay lines and it is proposed that attention
shall primarily be concentrated on their use for this purpose. As at
present planned the electronics will work at a rate of microseconds,
and the memory tubes will store the information for a millisecond, or
for any desired multiple of a millisecond.

Cartoon of Wilkinson and the Pilot ACE in 1952
Dr. Turing's proposals are set out in a paper
(E.882) considered at the March, 1946 meeting of the Executive
Committee of N.P.L. The Committee after discussing the problem with
Mr. Womersley, Superintendent of Mathematics Division, and Dr.
Turing, resolved unanimously to give the project its enthusiastic
support.
An example of the sort of problem that could be
solved is the calculation of ballistic trajectories. It is estimated
that a full trajectory from muzzle to strike, worked out by small
arcs, should be solved in half a minute. Or again a large number of
simultaneous equations, as in a geodetic survey, could be solved in a
few minutes: or the distribution of electric field round a charged
conductor of specified shape.
The complete machine will naturally be costly;
it is estimated that it may call for over £50,000, but probably
not twice as much. A smaller one, containing the essential
characteristics, could be constructed first, perhaps for a cost of
£10,000, but its chief function would be to reveal some of the
details of design that cannot be planned without trial, and its scope
would be too limited to be worth constructing for its own sake. This
would involve development work on delay lines and trigger circuits
and this part of the work would be undertaken by the Post Office
where facilities and specially trained staff exist, with the
collaboration of Dr. Turing and his assistants. The Post Office are
expecting to be able to profit by the development for their own
purposes.

Cartoon showing the NPL main gate
The small machine would not be a miniature
substitute for the large machine but would later constitute a part of
the full scale machine in due course. It is hoped that the complete
machine can be constructed in three years and the financial
requirement will be heaviest in the final year. It is proposed to
proceed immediately, and with high priority, in the design and
construction of this preliminary machine, but in doing so it is
important to know that if it fulfils its promise there will be full
backing for the greater sums required for the real operating machine.
In view of its rapidity of action, and of the ease with which it can
be switched over from one type of problem to another it is very
possible that the one machine would suffice to solve all the problems
that are demanded of it from the whole country. As far as can be
estimated at the moment, two Scientific and one Experimental Officer
will be required for this work in addition to Dr. Turing. Part of
this staff would work at the Post Office Research Station during the
development period. No estimate can as yet be given of the staff
required to use the machine when completed. This staff would,
however, in the main need to be in the Scientific Class since the
machine itself will do the work of a very large number of Laboratory
Assistants and Experimental Officers.
The Advisory Council of the DSIR agreed in May 1946 that 'in the
event of the first-stage machine fulfilling expectations, they would
be prepared to recommend further expenditure on a complete machine,
bringing the total up to perhaps £100,000 in the next three
years'. It only remained to build the computer. However, as a result of ineffective management this would take much longer than anyone expected.
17. Turing Pioneers Computer Programming

The ACE group outside the NPL's Babbage Building in 1948. From the left: Jim Wilkinson, Stanley Gill. Betty Curtis, Gerry Alway, Mike Woodger, Henry Norton. Photo taken by Donald Davies.

Michael Woodger and the ACE Simulator

Jim Wilkinson at the control panel of the Pilot ACE
In May 1946 James Wilkinson joined the NPL and was assigned to Turing
on a half-time basis. The ACE Section grew to a staff of three with the arrival of Michael
Woodger later that year. During 1946 Turing continually modified the design of the ACE. By the
time of Wilkinson's arrival Turing had reached what he called
'Version V' of the design. (Woodger explains: 'My
understanding is that the original report ['Proposed Electronic
Calculator'] was not a Version as such but a general proposal. There
is no trace of Versions I to IV; I assume they were sketches in
Turing's possession, probably done between March and May 1946.')
By the end of 1946 Turing had reached Version VII. From
December 1946 to February 1947 Turing and Wilkinson gave a series of
nine lectures on Versions V, VI and VII of the design (the lecture
notes are reproduced in Alan Turing's Automatic Computing Engine).
In 'Proposed Electronic Calculator' Turing had emphasized that work
on writing programs (i.e. 'instruction tables') should
'start almost immediately', since the 'earlier stages of the making of
instruction tables will have serious repercussions on the design' of
the ACE. Moreover, this policy would, he said, 'avoid some of the
delay between the delivery of the machine and the production of
results'. Turing made this point again in a letter to Darwin: 'A
large body of programming must be completed beforehand, if any
serious work is to be done on the machine when it is made'.' So it was that during 1946 Turing and Wilkinson, joined later by
Woodger, pioneered the science of computer programming. An
end-of-year report summarized their achievements:
Unless means can be found for the rapid
preparation of problems in a form suitable for the machine the value
of its high speed will largely be lost, though many other advantages
would still remain. The first step, therefore, in planning such a
machine, is to study the way in which programmes of work should be
prepared. This has formed the main work of the A.C.E. section during
the past year. It is intended to prepare the instructions to the
machine on Hollerith cards, and it is proposed to maintain a library
of these cards with programmes for standard operations. In setting up
the machine to do a particular job all that will be necessary
(instead of preparing the instructions in detail) will be to select a
number of groups of standard instructions and to link them together
with a few special cards. In planning the oganisation of the work on
the machine it has become clear that a long and careful study of the
many possible ways of setting out these instructions is essential,
and even after more than a year of work on this problem, the final
form is only now being reached. Apart from these general questions of
organisation a number of basic instruction routines have been decided
upon and prepared in detail. These are:-
- Division.
- Extracting square roots.
- Indication of failures.
- Testing the accuracy of a given table.
- Exponential function.
- Sine and cosine.
- Logarithm.
- Multiplication of complex numbers.
- Formation of scalar product of vectors.
- Formation of product of two matrices.
- Solution of sets of linear equations.
Some work has also been done on developing known
methods of solving both ordinary and partial differential equations
in a form suitable for use on the A.C.E.
All this work was, of course, directed toward a machine that existed
only on paper. The ACE Section, consisting only of three
mathematicians, had no facilities to construct the computer.
18. First Attempt to Build the ACE: the Flowers Era

T. H. Flowers

The Post Office Research Station at Dollis Hill, London. Here Flowers pioneered digital electronics and built Colossus.

Freddie Williams

Flowers lecturing at the NPL in 1977
Turing knew that Flowers, who had designed and built Colossus, was
uniquely qualified to undertake the construction of the ACE. Flowers
was asked to organize the building of the ACE at his headquarters,
the Post Office Research Station at Dollis Hill in North London
(where Colossus was built). He agreed. Early in 1946 Gordon Radley, Controller of Research at
Dollis Hill (who knew about Colossus), wrote to Womersley to
confirm the arrangement:
Thank you for your letter received on Saturday
morning. I had heard from Flowers that you were thinking of
constructing an electronic numerical computing machine at the N.P.L.
and share your hopes that it will far transcend in both facility and
speed anything previously attempted. We should be very happy to
co-operate, firstly by giving assistance with regard to the technical
design of the machine and, later on when this has taken shape, by
arranging to have it constructed for you within the Post Office
organisation... .
With regard to the other aspect, that of time,
we have very considerable arrears of work to overtake for our own
Department. Some of it is most urgently required and the manpower
position is difficult. I fully appreciate what you say, however, with
regard to the fascinating nature of the task and the prestige value
and it shall have the highest degree of priority possible in the
circumstances.
The 'arrears' mentioned by Radley were backlogs of urgent work on the
national telephone system (at that time managed by the Post Office).
Flowers could spare only two people to work on the ACE, Chandler and
Coombs (who were later to build the MOSAIC). His section was, Flowers said, 'too busy to do other people's
work'. By the summer of 1946 warning bells had begun to ring at the NPL. In
August Darwin observed that the Post Office was 'not in a position to
plunge very deep' and by November he was expressing concern to Radley
and others at the Post Office about the 'slow rate of progress' on
the ACE.Clearly it was time to make new arrangements. Initially the NPL
persisted with the idea of placing a contract for the construction of
the ACE with an outside organization. But this proved very difficult.
Engineers experienced in the new art of digital electronics were
scarce. Larger firms were 'likely to be too tied up with television
and other consumer goods', and a suitable smaller company could not
be found.
The NPL also attemped to enlist the help of other public
institutions. In August 1946 Darwin wrote to Sir Edward Appleton at
the DSIR concerning the possibility of the Telecommunications
Research Establishment at Malvern assisting in the construction of the ACE
(see chapter 11 The Manchester Computer):
As I told you Womersley was down at T.R.E. [Telecommunications Research Establishment] to see whether they could do any work about the A.C.E. machine. He tells me that it looks a most promising chance, and I think we should go ahead on it. Their lay-out for the job looks good, and I gather it appealed strongly to F. C. Williams as a job he would like to do, so that it should get a good chance. I am kicking myself for not having thought of it months ago as a possibility. ... It will be necessary to square T.R.E. officially over priorities, and on this I should like to bring high power to bear if necessary, because we have got a splendid chance of jumping in ahead of America.
In October 1946 Darwin himself visited TRE on NPL business and took the opportunity to bring up 'the possibility of F. C. Williams helping us on our ACE' (over two months after Womersley had made his initial approach—the pace of events was slow at the National Physical Laboratory). Darwin met Williams, who demonstrated the principles of cathode ray tube memory (see chapter 11 The Manchester Computer). Darwin realised that Williams' proposed memory was (in Darwin's own words) 'a most promising alternative ... more powerful than the mercury tubes, because its information would be available at need instead of only at fixed time intervals', and Darwin 'hoped that considerable assistance could be obtained' from Williams. Williams was sent a copy of Turing's 'Proposed Electronic Calculator' on Darwin's return to the NPL. Not long afterwards Darwin invited Williams, Uttley, and R. A. Smith (director of the Physics Department at TRE) to the NPL to meet with himself, Turing, and Womersley, in order to discuss 'in what way help could be given to the A.C.E. project'. The meeting took place on 21 November 1946. By that time, however, Williams had accepted the position of Professor of Electro-Technics at the University of Manchester, and shortly after the meeting Smith informed the NPL that, if Williams was to work on the ACE, it would be necessary to arrange a contract with the University. Darwin offered a contract, but in the end Williams declined. It was a pity—Williams would no doubt have got things moving on the hardware side. But on the other hand, Turing's design for the ACE was intimately based on the mercury delay line. An enforced collaboration between Turing and the pioneer of cathode ray tube memory might not have worked out well!

Maurice Wilkes with a set of delay lines from the EDSAC
The NPL also approached Maurice Wilkes, who was planning his own
computer at the Cambridge Mathematical Laboratory (the EDSAC, which
first ran in 1949). Douglas Hartree (Plummer Professor of Mathematical Physics at
Cambridge and a member of the NPL Executive Committee) sounded him
out and reported to the Executive Committee that Wilkes was 'prepared
to give as much help as he could on the ACE'. Wilkes 'had experience of making up [d]elay lines and would exchange
information with Dr. Turing', Hartree said. However, the chances of Turing's cooperating fruitfully with Wilkes
may be judged by a memo from Turing to Womersley:
I have read Wilkes' proposals for a pilot
machine, and agree with him as regards the desirability of the
construction of some such machine somewhere. I also agree with him as
regards the suitability of the number of delay lines he suggests. The
'code' which he suggests is however very contrary to the line of
development here, and much more in the American tradition of solving
one's difficulties by means of much equipment rather than thought. I
should imagine that to put his code (which is advertised as 'reduced
to the simplest possible form') into effect would require a very much
more complex control circuit than is proposed in our full-size
machine. Furthermore certain operations which we regard as more
fundamental than addition and multiplication have been omitted.
It might be argued that if one is to have so
little memory then it is necessary to have a complex control to make
up. In so far as this is true I would say that it is an argument for
either having no pilot model, or for not using it for serious
problems. It is clearly rank folly to develop a complex control
merely for the sake of the pilot model. I favour a model with a
control of negligible size which can later be expanded if desired.
Only test problems would be worked on the minimal machine.
By the beginning of 1947 there were no new initiatives to report.
'With regard to the design of actual equipment ... progress has been
slow owing to staff shortage' was the lame summary in the end-of-year
report for 1946. The slow pace of the construction work at Dollis Hill was not entirely the fault of the Post Office. As previously mentioned, during 1946 Turing kept changing the logical design of the machine, and the NPL even considered using cathode ray tube memory in place of mercury delay lines—a change that would have meant most of the work done by Chandler and Coombs was wasted. Coombs described the situation from the engineers' point of view:
One of the problems was, I remember, that NPL kept on changing its ideas, and every time we went down there and said 'Right now! What do you want us to make?', we'd find that the last idea, that they gave us last week, was old hat and they'd got a quite different one, and we couldn't get a consolidated idea at all until eventually we dug our toes in and said 'Stop! Tell us what to make'.
19. Second Attempt to Build the ACE: the Huskey Era and the Test
Assembly

Harry Huskey
The situation improved when Harry Huskey—an engineer—arrived
in Maths Division on a fixed-term contract. Huskey had worked on the
ENIAC project and in 1946 was offered the
Directorship of the EDVAC project, although complications prevented
him from accepting. Hartree, the ACE's guardian angel on the NPL Executive Committee, had
met Huskey while visiting the ENIAC in the spring of 1946; in July
Huskey received a telegram offering him a twelve-month visiting
position at the NPL. (Hartree was one of the few outsiders to know about Colossus; shortly after the end of the war Newman had invited him to Bletchley Park to look at Colossus.) Huskey began work in Maths Division on 4 January
1947. A number of other new recruits joined the ACE Section during the
course of 1947, in an expansion initiated by Turing (Gerald Alway in
August, Donald Davies in September, Henry Norton in October, Betty
Curtis in November).
Huskey soon suggested that the ACE Section itself make a start on
constructing the computer and he proposed to Womersley that a small
test assembly be built. With Womersley's blessing, Huskey, Wilkinson
and Woodger began work. They planned to build a simplified form of
Turing's Version V known as Version H (for 'Huskey'). The new
machine—soon called the 'Test Assembly'—was to be housed
in the Babbage Building, a short distance from Maths Division. Womersley summarized the situation in a report written in the middle
of 1947:
At the beginning of 1947 Dr. H. D. Huskey, a
member of the team working on the EDVAC and ENIAC machines at the
University of Pennsylvania, Philadelphia, joined the staff of the
Mathematics Division for one year. In the Spring of 1947 it was
decided that the Laboratory itself should undertake some experimental
work and Dr. Huskey, with two assistants, began the collection of
equipment with a view to constructing a small pilot model.
Turing was not in favour of this development. On the one hand the
Test Assembly was to be a small computer in its own right, involving
much more equipment than was strictly necessary to test the
fundamentals of Turing's design, and yet on the other it fell far
short of being the ACE, so possibly Turing saw Huskey's project as
diverting effort from his own. According to Wilkinson, Turing 'tended to ignore the Test
Assembly', simply 'standing to one side'. Woodger described how he 'was writing a program for [Version H] when
Turing came in ... looked over my shoulder and said, "What is
this? What's Version H?". So I said, "It's Huskey's."
"WHAT!" ... [T]here was a pretty good scene about
that'.
Huskey and the others pushed ahead with
the Test Assembly. By about the middle
of 1947, the NPL workshops were
fabricating a mercury delay line to Huskey's specifications, valve
types had been chosen and circuit block diagrams made, source and
destination decisions had been taken, and programs were being written
to check these decisions. A main frame was
built and construction of the
plug-in chassis holding the circuitry
was planned. Huskey's first goal was to run a simple stored program using
an absolute minimum of equipment and a single full-length delay
line. Then the group would develop a substantial computer capable of
solving practical problems; this would contain approximately thirteen
delay lines, and would involve punched card input and output and a
hardware multiplier. In October 1947 Womersley and E. C. Fieller expected—very
optimistically—that the Test Assembly would 'be ready by the
end of November'. (Huskey said: 'I never hoped to have the Test
Assembly working before I left in December. I certainly hoped the
group would have it working in 1948.')
Then, in what was one of the worst administrative decisions of the
whole ACE saga, Darwin summarily stopped the work. 'Morale in the
Mathematics Division collapsed', Huskey recalled. The man behind Darwin's decision was Horace Augustus Thomas, head of
the newly formed electronics group in the NPL's Radio Division.
20. Third Attempt to Build the ACE: the Disastrous Thomas Era

It has not been possible to locate a photograph of Thomas
In January 1947 Turing had gone to the United States, visiting
several of the groups that were attempting to build an electronic
stored-program computer. In his report on this visit he wrote:
One point concerning the form of organisation
struck me very strongly. The engineering development work was in
every case being done in the same building with the more mathematical
work. I am convinced that this is the right approach. It is not
possible for the two parts of the organisation to keep in
sufficiently close touch otherwise. They are too deeply
interdependent. We are frequently finding that we are held up due to
ignorance of some point which could be cleared up by a conversation
with the engineers, and the Post Office find similar difficulty; a
telephone conversation is seldom effective because we cannot use
diagrams. Probably more important are the points which are
misunderstood, but which would be cleared up if closer contact were
maintained, because they would come to light in casual discussion. It
is clear that we must have an engineering section at the ACE site
eventually, the sooner the better, I would say.
Darwin decided that NPL's Radio Division was the best place for the
experimental engineering work to be carried out. The minutes of the
March 1947 meeting of the Executive Committee outlined the new
arrangements:
A.C.E. Director reported that he had had
a meeting with members of the staff concerned. With a view to helping
on progress with this machine it had been suggested that Dr. Thomas
of Radio Division should be put in charge of the work of making by a
suitable firm a prototype model. Dr. Thomas was very keen on
electronic technique in industrial problems and he felt that the best
way in which we could get progress would be to have a pre-prototype
model started in Radio and Metrology workshops before approaching an
outside firm. It was agreed that Dr. Thomas should prove a very
suitable man for this work. In reply to a question from Professor
Hartree, Director said that Metrology and Radio workshops could get
on with the hardware part of the job straight away. Director stated
that he had had a letter from the Post Office giving the position of
their work which appeared to be most encouraging. Sir Edward Appleton
said that he had heard from Dr. Radley that they were finding it
difficult to keep to their delivery dates, and Dr. Radley will be
seeing Director about this.
The wheels of administration turned slowly and the idea of an
in-house electronics section took several months to implement. At the
end of April 1947 a joint minute to Darwin from Womersley and R. L.
Smith-Rose, Superintendent of Radio Division, suggested that
individuals be transferred from other Divisions to Radio Division in
order to form 'the nucleus of a future electronics section':
The present state of the project requires that
the group should work together in one place as a whole in close
contact with the planning staff in the Mathematics Division. The
various parts are so interwoven that it is not practicable at present
to farm out portions of the work to isolated groups. Our experience
with the Post Office confirms this... . The re-allocation of staff within the Laboratory requires ...
careful consideration, but if you are in agreement with our proposal,
could you advise us as to what action could be taken in the immediate
future.

The legendary Alan Blumlein, a pioneer of digital electronics. Blumlein was killed in an air crash during the war while testing his new radar system for bomber aircraft.

Blumlein in 1934
By August the months of 'careful consideration' finally came to an
end and notes were sent out by E. S. Hiscocks (the Secretary of the
NPL) to the Superintendents of various Divisions instructing them to
transfer staff to Radio Division for a period of six months.
Smith-Rose reported to Darwin: 'We are now in a position to commence
experimental work in the development of the A.C.E. for Mathematics
Division'. Two members of Maths Division (Gill and Wise) were transferred, and
Wilkinson, although not formally transferred, was expected by
Womersley to work with Thomas's group for the first few months of the
project. Edward Newman joined the group at the beginning of September. Recruited from EMI (Electric and Musical
Industries) Research Laboratories, Newman would play an
important role in the eventual construction of the Pilot ACE, as
would David Clayden, who followed Newman from EMI later that month.
Both Newman and Clayden were immersed in A. D. Blumlein's circuit
techniques, which they brought with them from EMI (see The Alan
Blumlein Homepage <www.AlanTuring.net/blumlein>).
In August 1947 a formal meeting was held to inaugurate the new state
of affairs:
A.C.E. Project
A meeting was held in the large Conference Room
on the 18th August to initiate the A.C.E. Project in the Radio
Division. The following were present:-
Director
Secretary
Superintendent, Radio Division
Superintendent, Mathematics Division
Mr. F. M. Colebrook
Dr. A. M. Turing
Mr. J. W. Christelow
Dr. H. A. Thomas
Dr. F. Aughtie
Dr. H. Huskey
Mr. M. A. Wright
Mr. W. Wilson
Mr. A. F. Brown
Mr. R. G. Chalmers
Mr. B. J. Byrne
Mr. R. F. Braybrook
Mr. A. I. Williams
The Director opened the meeting by stating that
this was the first time that a large team had been assembled at the
Laboratory to initiate a research programme, and stressed the
importance of the A.C.E. project. He pointed out that the Mathematics
Division was the parent Department, and that they had, as it were,
issued a contract to the Radio Division for the Development and
completion of the machine.
Mr. Womersley followed by giving a historical
summary commencing from the days of Babbage, and pointed out that the
N.P.L. project, if successful, would give a machine much in advance
of, and much quicker than, any of the American machines. It would
afford a new approach to the problems of Mathematical [Physics] and
would be of immense value to the country.
Even before the inaugural meeting, trouble was brewing behind the
scenes. On 12 August Hiscocks wrote to Darwin to alert him to what
seemed to be empire-building on Thomas's part:

David Clayden

Thomas has apparently shown some signs of
behaving as if he is starting up a new Division, and so as to allay
certain qualms which both Smith-Rose and Womersley have, I think it
would be better for it to be explained to the whole team that
Mathematics Division is the parent Division, and the one which is to
justify the financial outlay on this work; that the work is being put
out on contract, as it were, to Radio Division, and that Thomas's
team is a part of Radio Division. I think, even if only for our own
peace of mind, this is desirable, because Thomas has already shown
some signs of wanting to set up a separate office, etc.
An unfortunate rivalry quickly sprang up between Thomas's group and
the ACE Section in Maths Division. On 17 September Smith-Rose was
sent an indignant letter complaining about a raid by Thomas's group
on the ACE Section:
During Dr. Turing's and Dr. Huskey's absence on
leave, most of the apparatus in our laboratory in Teddington Hall
has, I believe, been removed to your Division. It would be of
assistance in maintaining our inventory if we could have a list of
what was, in fact, taken; we understood from Dr. Huskey that only two
items were to be moved.
Thomas the empire-builder soon petitioned Darwin to curtail the
construction work in the ACE Section. Wilkinson said in an interview
given in 1976: 'Thomas particularly didn't like ... the idea of this
group in Mathematics Division ... working independently ... . Thomas
persuaded the Director to lay it down that all work should be done in
the Electronics Section and Darwin decreed that we should stop work
on the Test Assembly'.
The result was that the construction of the ACE drew almost to a
standstill. Although Newman and Clayden were skilled in digital
techniques, Thomas's group had much to learn. Thomas's own background
was not in digital electronics at all but in radio and industrial
electronics. The group 'began to develop their knowledge of pulse
techniques', said Wilkinson, and 'for a while they just did basic
things and became more familiar with the electronics they needed to
learn to build a computer'.Then, in February 1948, Thomas delivered another blow to the ACE
project, resigning from the NPL to join Unilever Ltd (the
manufacturers of 'Sunlight' soap). As Womersley summed up the
situation shortly afterwards, hardware development was 'probably as
far advanced 18 months ago'.
It seems probable that, given better management at the NPL, a
minimal computer based on Turing's Version V could have run a program
during 1948. Turing first proposed an in-house electronics section at
the NPL in his report of 3 February 1947. The Radio Division group
could have been set up in six weeks rather than six months. Clearly
the new electronics group should have joined forces with Huskey and
the ACE Section to work on the Test Assembly.
In August 1947 Womersley had pressed for this course of
action, but Thomas threw a spanner in the works. A rudimentary form of the Test Assembly might easily have run a trial
program before the middle of 1948, becoming the world's first electronic
stored-program digital computer.
21. Turing Leaves the NPL

In mid-1947 Turing applied for a period of sabbatical leave to be
spent at his Cambridge college. He proposed to pursue research on
machine intelligence. Darwin approved the request, saying in a letter to the DSIR:
As you know Dr. A. Turing ...
is the mathematician who has designed the theoretical part of our big
computing engine. This has now got to the stage of ironmongery, and
so for the time the chief work on it is passing into other hands. I
have discussed the matter both with Womersley and with Turing, and we
are agreed that it would be best that Turing should go off it for a
spell.
Turing left for Cambridge in the autumn of 1947. He returned briefly to Mathematics Division the following spring
(winning the three-mile run at the NPL Annual Sports Event). Then, in May 1948, no doubt disheartened by the complete absence of
progress on the construction of the ACE, he gave up his job at the
NPL, accepting Newman's offer of a position at the Manchester
Computing Machine Laboratory (see chapter 13 Turing Joins the
Manchester Project). The struggle to bring the ACE into existence was
now led by Wilkinson.
22. Fourth Attempt to Build the ACE: the Wilkinson-Colebrook Era
and the Pilot Model

The Daily Telegraph, 31 January 1950

The Pilot Model ACE in 1950, with (from left) Edward Newman, Francis Morley Colebrook, James Wilkinson, and Donald Davies

The Pilot Model ACE in 1950, with Gerald Alway (left) at the Hollerith card input/output equipment, James Wilkinson (centre) at the control panel, and Edward Newman (right) at the main panel
Thomas was replaced by Francis Morley Colebrook, who in March 1948
was made head of the newly designated Electronics Section of Radio
Division. Colebrook at last got things moving. In 1976 Wilkinson recollected:
I think quite soon [Colebrook] had an
uncomfortable feeling that he'd inherited something which was in
danger of floundering, and I had the same feeling back in Maths
Division - I'd inherited this team from Turing and everybody was
really a little bit demoralised by that time. And Colebrook rang me
up and he came over to see me and had a chat about it and said he was
not very happy about the position. And ...
to my absolute astonishment he said: 'I've got a suggestion to make
... You chaps have learned
a bit of electronics now ...
What about coming over and joining us and the two groups working
together?' ... I felt the
whole thing was in such a mess it needed quite a decisive break in
order to get it going... . Colebrook ... was a great
diplomat ... and his
goodwill was so evident to everybody that I do think he played a
major part in making it possible for the two groups to go together.
The combined group decided that the best course of action was to
revive the Test Assembly, now described as a 'pilot model'. (The similarity between the pilot model they now worked on and the
out-of-favour Test Assembly was, Wilkinson said, 'more than ... it
was diplomatic to say much about'.)
The ACE Section and the Electronics Section worked harmoniously
together, and at the end of the year Womersley was able to report
that '[v]ery good progress has been made'. Huskey's approach to circuit design was replaced by the Blumlein
approach which Newman and Clayden had brought from EMI. The group
completely redesigned the electronics of the machine.
Soon the mathematicians from the ACE Section found themselves in a
novel milieu. Woodger recalled: 'We set ourselves up in a little
assembly line with ... a stack of components ... in front of us. Each
of us had a soldering iron and we produced these things and passed
them down the line. Oh, it was tremendous fun'. Following a period of difficulty with the delay-line amplifiers at
the end of 1949,
the group finally tasted success. On 10 May 1950 the Pilot Model ACE ran its first program. Later known affectionately
as 'Succ. Digs' (successive digits), the program turned on a row of
32 lights on the control panel at a speed determined by size of the
number on the input switches.
The Pilot Model ACE was (in Colebrook's words) 'powerful computing
equipment'. Although the ultimate goal remained a large-scale ACE, Maths Division
had been planning since 1948 to use the Pilot Model as a computing
machine in its own right. However, there was still considerable work to be done before the
Pilot ACE could be handed over to Maths Division for customer
service. Unreliable components were a problem and it was September
1950 before the machine had an error-free run of half an hour. During 1951 the delay lines and the control of input and output were
redesigned and the parallel multiplier was added. By about the middle of 1951 the Pilot ACE was doing over fifty per
cent of the computing work of Maths Division. Nevertheless, by October 1951 it had still 'not yet been put into
regular service', said Colebrook, 'and we have not yet built up an
adequate "library" of generally useful sub-routines'.
At the end of October 1951 the new Director of the NPL, Sir Edward
Bullard, expressed the opinion that
most of the electronic machines, including our
own, do not really work regularly and reliably. They have been very
much over-advertised and there is a lot of work to be done before we
have anything that is much use.
Despite Bullard's pessimism, by February 1952 the Pilot ACE was
reliable enough to be dismantled and transferred to Maths Division. Colebrook wrote:
Full operation was resumed within two weeks
after the removal and has been continuous ever since, mainly on
defence problems... . An
analysis of the first eight weeks of operation, involving 370
power-on hours, gives the following figures:-
| Routine testing and maintenance |
92 hrs. 25% |
⎫
⎬
⎭ |
|
| User training, programme testing, etc. |
175 hrs. 47% |
75% |
| Paid-for work |
103 hrs. 28% |
|
The Pilot ACE was a huge success. It was used both to carry out
research in numerical analysis and to do paid work through
Mathematics Division's scientific computing service. In 1954 alone
the Pilot ACE earned the NPL £24,000 for over 80 jobs—Turing's
annual salary when he designed the ACE was £800. In the course of its working life the machine
earned approximately £100,000. The Pilot ACE remained in continuous service until replaced by the
first DEUCE in
1955, by which time 'the amount of maintenance
it require[d] preclude[d] it from being used economically as a
computer'.
23. The DEUCE

This DEUCE, photographed in 1956, was installed at the National Physical Laboratory in 1955

This DEUCE, known as the UTECOM, was situated at the New South Wales University of Technology in Sydney, Australia (UTECOM stood for 'University of Technology Computer')

Control panel of the UTECOM. The topmost row of 13 white lights displayed the current instruction. The two circular monitors to the right displayed the contents of delay lines. The large device standing to the left of the control panel is the Hollerith card reader. Each program was entered in the form of a deck of many punched cards.

UTECOM playing noughts and crosses
Towards the end of 1948, the NPL's efforts to find an engineering
company willing to assist with the ACE at last bore fruit. The
minutes of the NPL Executive Committee for September 1948 report:
In connection with the A.C.E., members of Sir
George Nelson's staff have visited the Laboratory to see the progress
made and to discuss possible collaboration in the more detailed
design and, later, the construction of the A.C.E.
Nelson, chairman of the English Electric
Company, had been a member of the NPL Executive Committee since 1946
(and was present when Turing addressed the historic meeting of March
1946). Early in 1949 it was proposed that the NPL place a contract
with English Electric:
A.C.E. Project.
Present Position, and request for financial
provision for a Study Contract to be placed with the English Electric
Co. Ltd.
... In
order to expedite the construction of [the] pilot assembly and to
make possible the construction of the final machine it is now
proposed that a Study Contract be placed with the English Electric
Co. Ltd. This will have two great advantages, first it will add to
the labour force working on the construction of the pilot model, and
should make possible its completion before the end of this year, and
it will familiarise the engineers and the staff with the specialised
requirements and the techniques involved. This educational period
before they embark upon the construction of the final machine is very
necessary in view of the novelty of the whole enterprise.
This contract was approved by the Treasury in May 1949. It 'provided for members of the English Electric Company staff to
work at the N.P.L., with N.P.L. staff involved'. Engineers and wiremen from English Electric joined the NPL team to
assist in the completion of the Pilot ACE.
In 1951 an NPL memorandum set out a number of reasons for desiring
to 'continue the collaboration with the E.E.Co.', including the
following: 'The experience gained by the E.E.Co. would enable them to
reproduce the A.C.E. or a similar machine for any subsequent home or
foreign demand'. By December 1951 arrangements for producing a commercial version of
the Pilot ACE had been firmed up:
ACE - Arrangements with English Electric Co.
...
[I]t has been decided that the first move shall be the construction
by the E.E. Co. of an “engineered version” of the present
Pilot ACE. Simultaneously with this some of the detailed planning and
design for the full-scale ACE will be undertaken.
A memo from Treasury noted approvingly that
These plans for the development of the A.C.E.
represent a very favourable turn. English Electric (through Sir
George Nelson) offered to take it upon themselves to construct a
properly “engineered” version of the Pilot model at a
cost to N.P.L. of no more than f5,000... . The likelihood is that [this] by no means represents the full
economic cost. But Sir George Nelson is prepared to think in terms of
such a figure because he would like to see English Electric getting
into the field.
The engineered version of the Pilot ACE was called—naturally
enough—'the DEUCE' (Digital Electronic Universal Computing
Engine). The first DEUCE to be
produced was delivered to Maths Division in March 1955. The DEUCE went on to become a cornerstone of the
fledgling British computer industry.
24. The Big ACE

Work begins on the Big ACE. First the engineers constructed this mock-up of the layout
Work began on a full-scale ACE in the autumn of 1954. In 1956 J. R. Illingworth outlined the reasons for proceeding to this
final stage of the project:
ACE - Final Model
...
Experience had already shown ...
that the DEUCE would not be an efficient proposition for more than
four or five years since the speed and storage facilities required
for this type of machine were becoming greater year by year. It was
therefore decided about two years ago to commence work on an entirely
new machine and this started in the Autumn of 1954... .
The whole position, I think, may be summed up
by saying that both the importance and the significance of this work
has changed. In the early days when the project was envisaged it was
not even known whether the conception of the ACE would lead to a
research “toy” of any value, whereas events have proved
it to be such a first class computing mechanism that we are under
pressure from the Treasury and other departments to develop its use
as rapidly as possible for work in office mechanisation. Moreover,
whereas in the early days the project was regarded as an additional
facet to the Laboratory's normal work, the whole of this field of
work has become an inherent part of the Laboratory's programme.
Built and housed at the NPL, the Big ACE was in operation by late
1958. Only one was made. Wilkinson, Clayden, Davies, Newman, and
Woodger all contributed to the final design. (English Electric played a part in 1954 and 1955 during the
developmental stage, but at that point their contract with the NPL
came to an end.)
With a clock speed of 1.5 MHz and containing some 6000 valves, the
Big ACE filled a room the size of an auditorium. The computer remained in service until 1967.

The Big ACE, November 1958. Raised panels expose the racks of chassis.
At a Press Day held in 1958 to inaugurate the Big ACE, A. M. Uttley
(Superintendent of the Control Mechanisms and Electronics Division,
as the Electronics Section had by then become) announced: 'Today,
Turing's dream has come true'. If so, it was a dream whose time had passed. The Big ACE was not the
revolutionary machine that it would have been if completed six or
seven years earlier. Not only did it employ valves in the era of the
transistor, the designers also retained the by then outmoded mercury
delay line memory proposed by Turing in 1945. Nevertheless, the Big ACE was a fast machine with a large memory, and
the decision to stick with the principles used in the Pilot ACE and
the DEUCE was reasonable in the circumstances. In 1953 Colebrook
urged that the proposed full-scale ACE 'be based on well proved
components and techniques, even when revolutionary developments seem
to be just around the corner'. 'Otherwise the [Mathematics] Division will get nothing but a
succession of pilot models', Colebrook argued. As for speed, the machine's designers wrote in 1957: 'The ACE appears
in fact to be about as fast as present-day parallel core-store
computers' (magnetic core memory was the most advanced high-speed
storage medium at that time).

Donald Davies, co-author of 'A Simple Guide to ACE'. Subsequently Davies invented 'packet switching', used in the ARPANET, forerunner of the Internet.

Early chassis for the Big ACE, 1956
A Simple Guide to ACE
One of the world's largest and fastest
electronic computing machines - popularly called 'Electronic Brains'
- has begun to operate at the National Physical Laboratory. Its name
is ACE - and it can carry out any calculation process for which exact
rules are known... .
ACE incorporates many unique design features.
The operating “mechanism” consists of about 6,000
miniature electronic valves, arranged in an impressive array of 10
large cabinets. Each cabinet is fitted with an electrically operated
rising door to give rapid access for fault finding. It has a cooling
system of circulating air, with heat exchangers and a water cooler.
The numbers and instructions have 48 binary
digits (equivalent to 14 decimal digits). The working store consists
of 800 words, and the backing store of four magnetic drums will
contain a total of 32,768 words.
Mercury delay lines and magnetic drums are used
for the storage of numerical data and instruction sequences, and both
punched card and magnetic tape equipment are provided for input and
output.
The compact control desk has some 160 keys and
300 signal lamps, in addition to audible and visual displays of the
computation. Nevertheless, most computations are carried out entirely
by pushing one key - marked “Initial Input”. This key
causes punched cards to be read, which tell ACE what to do.
The most interesting mechanical assemblies in
ACE are the four magnetic drums, entirely designed and constructed at
N.P.L. The drums rotate at 12,000 r.p.m. so accurately that the
arrival at a given point of a magnetic spot one hundredth of an inch
in length, travelling at 200 miles per hour, is timed to a millionth
of a second. The drums have unique rapidly moving recording heads and
are only a part of the number store or “memory” of ACE.
An idea of the speed of ACE can be gained from the fact that these
drums are the slowest part of its number store!

128 track magnetic drum for the ACE Pilot Model, 1954
Technical Notes
ACE has three forms of storage. The largest
part of the store consists of four magnetic drums... . The access to these numbers is limited by the need to wait for the
drum to revolve, and may take up to 7 milliseconds. These drums are
used by the computer for the large mass of data that it may not want
quickly.
For more rapid access, a mercury delay line
store of 768 numbers is employed. The time required for access to
these is up to one millisecond. This store is used for the program,
but instructions are stored in such a way that no time is wasted in
waiting for them.
The most rapid access store consists of short
delay lines storing one, two or four numbers each. These are used for
the small group of numbers that the computer is using for a short
while.
By good programming, the full advantages of the
large store can be enjoyed, with a time of access not much greater
than is given by the short delay lines.
The ACE instructions specify the addresses -
the locations in the store - of two numbers to be operated on, the
operation, and the addresses of the desired destination of the result
and of the location of the next instruction. Thus four addresses are
used, and all four accesses occur nearly simultaneously.
[M]ultiplication and division occur in separate, autonomous devices,
so that they can occur simultaneously with other operations.
In many cases, the computer will average 15,000
operations per second, each involving extracting two operands,
storing the result and extracting the next instruction.

Turing
Input and output is by punched cards. Magnetic
tapes will be fitted later, but will be used as an extension to the
store. The input speed from cards will be 7000 binary digits per
second, with a rate of 450 cards per minute punched in binary.
25. Conclusion
Turing's 1936 paper 'On Computable Numbers' gave the world the
fundamental ingredients of the modern computer: the stored program
concept and the concept of a universal machine.
In the United States, von Neumann placed Turing's concept of a
stored-program universal computer into the hands of the electronic
engineers who would build the first American machines.
The 1936 paper profoundly influenced Newman, in whose Computing
Machine Laboratory at Manchester in 1948 the first functioning electronic
stored-program computer came to life. Turing taught Kilburn, the designer of this machine, the fundamentals of computer architecture in lectures in 1946-7.
Turing's own sophisticated ACE design found commercial success in the DEUCE. Based on Version V of Turing's design,
the DEUCE was a major workhorse of the first decades of the computer
age. The first single-user, desk-side computer—the first personal
computer—was also based on the ACE design (Huskey's G15). More yet would have flowed from Turing's ACE design had there been
effective management at the National Physical Laboratory. Huskey's
minimal ACE (the Test Assembly) might well have been the first
electronic stored-program computer.
In addition to his remarkable theoretical and practical contributions
to the development of the computer, Turing was the first pioneer of
the areas of computing now known as Artificial Intelligence and Artificial Life.

Turing
Picture Credits
Notes
The quotation is from Good's revised typescript of his acceptance speech delivered on 15 October 1998, p. 31. (Good sent Copeland a copy of this typescript in January 1999.)
















































































 Tom Kilburn posing in front of the 1998 rebuild of the Manchester Baby Photo © Carolyn Djanogly.
Tom Kilburn posing in front of the 1998 rebuild of the Manchester Baby Photo © Carolyn Djanogly.  The Pilot Model of Turing's ACE in 1952
The Pilot Model of Turing's ACE in 1952 Turing
Turing



















































