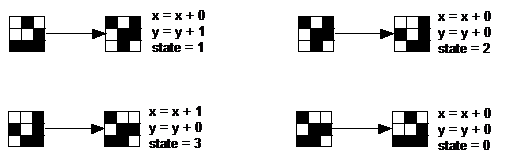The Existence of Software
Eric Steinhart
Introduction
Although software objects are pervasive in modern computerized societies, little logically rigorous work has been done on their nature. Work by Suber (1988) and Colburn (1999) is preliminary and not directly ontological. Much that has been written on software objects is confused. For example, Hailperin et al. (1999) say software objects are "concrete abstractions". Many writers treat software objects as abstract objects of some sort. They are "embodied" or "realized" or "instantiated" in hardware. For instance, Sloman (1993) says that software objects are non-physical.1 But that is false. A computer virus is physical. A word-processing document stored on your hard drive is physical. Software objects have locations and are made of real mass-energy. If your computer is an electronic digital computer (a von Neumann machine), then all the software objects in your computer are made of electricity. Software is physical.2
Although hardware and software are both physical, it is still useful to draw a distinction between them. Hardware objects are the lowest level machines in some physical system. The coordinated interactions of lower level machines can support the existence of higher level machines. Software objects are higher level machines. These higher level machines are patterns (in a technical sense) in the interactions of the lower level machines. Simpler software objects can be assembled to make more complex software objects at higher levels. We use the Game of Life to illustrate levels of machines. We discuss applications to actual physics. If certain field theories are right, then electrons (and other basic material particles) are software machines. They are obviously physical. We examine the idea that the mind is to the brain (or the person is to the body) as software is to hardware.
The Game of Life
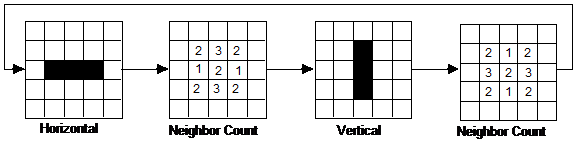
A Game of Life is a network of machines (Poundstone, 1985). It is played on a grid composed of square cells, like a chessboard. A clock is ticking (all cells can hear it). A cell is either ON or OFF (alternatively, LIVE or DEAD, or 1 and 0). Each cell is little computer that gets input from its neighbors. So the grid of cells (the life grid) is a computer network. Cells blink ON and OFF like light bulbs. They change their states according to a rule each cell computes every time the clock ticks: (1) a cell counts its ON neighbors; (2) if it is ON and has 2 or 3 ON neighbors, then it stays ON, else it turns OFF; if it is OFF and has 3 ON neighbors, then it turns ON, else it stays OFF.The Game of Life rule is encoded in the state-transition table in Table 1. Figure 1 illustrates how the rule acts on a horizontal bar of three ON cells. The rule changes the horizontal bar into a vertical bar. The rule then changes that vertical bar back into a horizontal bar. The oscillating bar of three ON cells is known as the blinker. Figure 2 shows a pattern of cells that moves. This mobile pattern is the glider. Although it looks like the cells in the glider are moving, they are not. The cells stay put. The motion of the glider is the motion of a higher level object – a software object. It is like the motion of a pattern of light values on a scoreboard. The pattern of light values moves although the light bulbs stay put. The glider is a simple machine. There are many other kinds of simple machines in the Game of Life. You can build more complex machines out of simpler machines. These machines can be of arbitrarily high finite complexity. Several researchers have shown how to build universal computers on the life grid (universal Turing machines and register machines).
You can easily find programs that let you run the Game of Life on a personal computer. You distribute ON values to the life grid and hit the start button. You watch the distribution change. Setting up a Game of Life is like setting up a little universe. Watching it run is like watching a universe evolve. The distribution of ON cells is the initial condition of your little life universe. The Game of Life rule is the most basic physical law. A Game of Life is a simple example of what Quine called a Democritean world (1969: 147 – 155). It is a kind of computer game known as a cellular automaton (Toffoli & Margolus, 1987). Any cellular automaton is a cellular universe. Many writers have argued that our universe is a cellular universe (Fredkin, Landauer, & Toffoli, 1982; Fredkin, 1991; Zeilinger, 1999; Steinhart, 1998). And even if our universe isn’t a cellular automaton, there are plenty of ways for networks of computing machines to approach the complexity of our universe. Our universe might be realized by a network of computers.
Formal analysis of lowest level machines in the Game of Life
At any moment, a Game of Life is played on a life grid. A life grid has two spatial dimensions and one temporal dimension. All dimensions are infinite in both directions and are discrete. We identify each dimension with the set Z of integers. So the life grid is the set of space-time points (x, y, t) where x and y and t are all from Z.
A lowest level machine is located at each point in the life grid. Each lowest level machine has four properties. These are: its program P; the location of its center on the x axis; the location of its center on the y axis; and its state.3 A machine is minimally extended in space and in time. Machines do not endure through time. A machine has a previous (past) temporal counterpart and a next (future) temporal counterpart. If a machine is located at (x, y, t), then its previous counterpart is located at (x, y, t-1) and its next counterpart is located at (x, y, t+1). A history of a machine is the set of all counterparts to which it is linked (transitively) by its past and future counterpart relations. The program is essential to the machine. Its counterparts must run the same program. The x and y locations are also essential. Since lowest level machines don’t move, they stay the same. The current state is accidental. It can vary from counterpart to counterpart. If a machine is in state s and gets input i, then the state of its next counterpart is determined by its program.
Any precise description of the Game of Life is heavily committed to set theory. So we formalize this as an official set theoretic hierarchy. The machines are the lowest level individuals in this hierarchy. The set of machines is V0. The hierarchy is cumulative. Each next level Vn+1 is the union of Vn with the power set of Vn. Since we’ve accepted an infinitely extended life grid, we need at least the first transfinite number ω. So we need to affirm at least the first limit level Vω. And since we need functions and so on over the whole life grid, we need at least a few levels of sets above Vω. We probably don’t have to go beyond Vω+ω. But if we’re going into the infinite, there’s really no reason to stop. We thus posit a level Vn for every ordinal definable in ZFC.
A machine has current state either 0 or 1. We can abstract from these machines to consider a purely geometrical representation of the Game of Life. Since the machines are located at points, and since they have states, the machines define a field of states. It is a binary scalar field. The field of states is made of cells. A cell is a quad (x, y, t, v). The items x, y, and t are coordinates while the item v is the state of the machine at (x, y, t). So we can define a Game of Life G as a set of cells whose values satisfy the Game of Life rule.
An event in some Game of Life G is any set of cells that all have the same temporal coordinate. An event is minimally temporally extended. An event doesn’t have to be the whole life grid. It can be cropped to include only some proper part of the grid. For instance, the set of ON cells in some glider is an event. A process in some Game of Life is any temporally ordered series of events. We are only interested in processes that are temporally extended (that contain more than one event and that are temporally continuous (each next event in the process occurs at the next time).
Material things and programs
The matter in a thing (its materiality) is traditionally defined both as (1) that which remains invariant through change and (2) that which individuates the form of the thing. The individuation is done by the space-time location of a thing. The invariance through change is done by some regularity in the physical detail of the thing. The regularity must be independent of the Game of Life rule (the basic causal law of the Game of Life). It must be a regularity of the thing rather than a global regularity of space-time.
A material regularity is a pattern in the physical detail of a process. The physical detail of a process contains a pattern iff it is algorithmically compressible (Chaitin, 1975; Dennett, 1991). It contains a pattern iff there is some program that takes as input some event in the process (typically the initial event) and generates the other events in the process without reference to the causal laws that govern the basic fields. A pattern is thus a dynamical universal. A pattern is a program (described in a programming language).
Every type of material thing has an program that defines its invariances. The program specifies “that which remains the same”. One of the most basic invariants is shape. For example: in the Game of Life, processes like blocks, blinkers, and gliders are “things” because they are shape-preserving and because simple programs suffice to generate all their detail. But the explosive chaos of the r-pentomino is not a thing. There is no shape-preservation or regularity in that explosion. The only way to generate the explosion of the r-pentomino is to run it using the basic causal law of the life grid.
A material thing is a process with a persistence relation defined by an algorithm that (1) takes as input some space-time location that individuates the thing; and (2) transforms the initial shape of the thing according to some algorithm that is independent of the causal laws of the basic fields. For example: consider a blinker. A blinker is centered on some point (x, y). A blinker is just a rotating bar. At each time step of the life grid, it rotates 90-degrees clockwise (do it counterclockwise if you like). A blinker thus has two states. We’ll say state 0 is horizontal and state 1 is vertical. The history of a blinker can be defined by an algorithm Blinker that does not depend on the basic causal law of the Game of Life. The algorithm takes a center and state as inputs. It also takes as input some number n of steps to run the blinker. So the algorithm is Blinker( x, y, state, n).4 The output of Blinker at each time is just the pattern that it writes on the life grid. Let Alpha and Beta be patterns on the life grid. Beta is later than Alpha. If P is a pattern, then the center of P has coordinates P.x and P.y. The state of P is P.state. Any pattern generated by the application of Blinker to an initial blinker pattern is the same blinker. Thus persistence for the blinker is:
Beta is the same blinker as Alpha iff there exists n
such that Beta = Blinker( Alpha.x, Alpha.y, Alpha.state, n).
Consider the glider. The glider is a moving pattern in the Game of Life. The glider is an example of a particle-like wave (Adamatzky, 1998). It is a thing because it is shape-invariant. It preserves its shape through changes in position. You can picture the glider as a doing a kind of corkscrew rotation that is counterclockwise in the direction of its motion. The motion of a glider can be defined by a program Glider that does not depend on the basic causal law of Game of Life. The program takes as inputs a center point, a state, and the number of steps to run the glider. So the algorithm is Glider( x, y, state, n).5 The output of the Glider program at each time is just the pattern that it writes on the life grid at that time. Diachronic sameness (persistence) for the glider is:
Beta is the same glider as Alpha iff there exists n such that Beta = Glider( Alpha.x, Alpha.y, Alpha.state, n).
5. Rules and State-Transition Networks
An event has a shape. An event Alpha is the same shape as an event Beta iff there is some shift that changes all the cells in Alpha into identical cells in Beta (and vice versa). A shift includes any translations (any movements in either the x or y direction and in the t direction). A shift does not include any rotations or reflections. The same shift is applied to all cells in the event. For instance, we shift Alpha right 1 (by adding 1 to the x coordinates of all cells in Alpha) and down 1 (by adding 1 to all the y coordinates in Alpha) and to the future 4 (by adding 4 to the time coordinates of all cells in Alpha). If the result of this shift (+1, +1, +4) is Beta, then Alpha is the same shape as Beta (and vice versa). The sameness of shape relation is an equivalence relation. Sameness of shape partitions the set of events into equivalence classes. These equivalence classes are shapes.
At the level of shapes, the Game of Life rule transforms one shape into another shape. A series of transformations is a loop (or cycle) if the last shape in the series is identical to the first shape in the series. A loop corresponds to an invariant in the Game of Life rule at the level of shapes.6 If n transformations turn a shape S back into S, then S is invariant under n transformations. For instance, the blinker is invariant under 2 transformations.
We can express a loop as a series of rules. We assign a state number to each shape in the loop. The initial shape in the loop has state = 0. The transformation of one state into the next state can move it spatially on the life grid. We need to explicitly indicate the move by indicating changes to the x and y coordinates of the shape. A rule thus has the following form: if (state = n) then { change x; change y; change state; }.
Figure 3 shows the rules for the loop of the blinker. It is a loop with two states. State 0 is the vertical bar of 3 on cells. State 1 is the horizontal bar of 3 on cells. Since the blinker does not move, the updates for the x and y coordinates add 0. The first rule (on the left in Figure 3) reads like this: if (the blinker is vertical) then { there is no x shift; there is no y shift; the blinker changes to horizontal }.
Figure 4 shows the rules for the loop of the glider. It is a loop with four states. These are the familiar glider states. Since the glider moves, the updates for the x and y coordinates sometimes add 1. The first rule (on the upper left in Figure 3) reads like this: if (the glider is in state 0) then { there is no x shift; shift the glider down 1 on the y axis; change the state to state 1; }. The consequent of the rule is equivalent to an instruction for writing the state on the life grid. The series of four rules changes the shape back into state 0.
The cycles of the blinker and glider are very simple. They go through their changes without any input from the outside environment. They do not interact with any other shapes. A more complex kind of cycle involves the interaction of two shapes. The first shape is the one that will remain invariant through the interaction (it will be the same at the end of the cycle). The second shape is the input to the first shape. Consider the eater. If it remains by itself, the eater is stable like the block. If it remains by itself, the eater is a loop of length 1. But if a glider approaches from the northeast, then the eater goes through a series of transitions that takes it back to its stable form. It goes through a cycle of length 4. Figure 5 shows these two cycles of the eater as a state-transition diagram. The rules that define the eater take inputs. They have this form: if (state = n and input = i) then { change x; change y; change state; }. The input and state are shapes with the same center. All machines in the game of life can be defined using rules of this general form.
The cycles of the blinker and glider are very simple. They go through their changes without any input from the outside environment. They do not interact with any other shapes. A more complex kind of cycle involves the interaction of two shapes. The first shape is the one that will remain invariant through the interaction (it will be the same at the end of the cycle). The second shape is the input to the first shape. Consider the eater. If it remains by itself, the eater is stable like the block. If it remains by itself, the eater is a loop of length 1. But if a glider approaches from the northeast, then the eater goes through a series of transitions that takes it back to its stable form. It goes through a cycle of length 4. Figure 5 shows these two cycles of the eater as a state-transition diagram. The rules that define the eater take inputs. They have this form: if (state = n and input = i) then { change x; change y; change state; }. The input and state are shapes with the same center. All machines in the game of life can be defined using rules of this general form.
A state-transition network is connected iff there is a path from any state in the network to any other state in the network. A program is a connected state-transition network. The simplest programs are state-transition networks with a single cycle. For example, the state-transition networks for the glider and blinker all have one cycle. More complex programs have many cycles radiating from a single central shape. For example, the eater has two cycles radiating from state 0. Even more complex programs have many intersecting cycles radiating from many states. We can think of programs in terms of dynamical systems theory. The state-transition network of a program is an attractor basin.
6. Formal analysis of higher level machines in the Game of Life
A process is running a program P iff the shape of the initial event in the process is one of the states of P and all the later events in the process are generated by transitions in P. An event is running a program P iff it is an initial event in some process that is running P. Since a process is of length greater than 1, an event is running a program if and only if the event makes a transition in the program to another event. It follows that the last event in a process does not run a program (the program ends at the last event).
A higher level machine has four properties. These are: its program P; the location of its center on the x axis; the location of its center on the y axis; and its state. If the existence of a higher level machine is revealed by a program, then we get this axiom:
Existence Axiom for Higher Level Machines:
For every Game of Life G, for every
event in G,
if the event is running a program P,
then there exists a higher
level
machine M
that is located at the event.
A higher level machine is not an abstract object. It is a concrete object (in the sense that it has a space-time location and causal powers). Every higher level machine M is located at some event S and its causal powers are the transitions in the program P. Every higher level machine is a physical thing. Since a higher level machine is located at an event, and since events are minimally temporally extended, higher level machines are minimally temporally extended. They do not endure. If a process is running a program, then there is a temporal counterpart relation that connects the machines located at the events in that process. Since higher level machines are physical, they are individuals in V0. The programs for higher level machines are autonomous. They are not defined in terms of and do not depend on the life rule. The Game of Life rule does not appear in any higher level program. You could use them to make a process without knowing anything about the Game of Life. Although these programs are motivated by studying regularities in the Game of Life, we can treat them as independent primitive elements in an entirely novel game.
The Game of Life contains many simple higher level machines. These are first level machines. They include still lifes (e.g. the blinker). They include simple oscillators (e.g. the blinker). The include simple movers (e.g. the glider, spaceships). They include conditional machines like the eater. Simpler machines can be assembled to make more complex machines. The more complex machines are at higher levels. As simpler machines are assembled into higher level machines, a hierarchy of machines emerges.
For instance, four blinkers can be assembled to make a stoplight. The stoplight is a second level machine. Two blocks and a shuttle can be assembled to make a second level oscillator (Poundstone, 1985: 88). Four blocks and two B heptomino shuttles can be assembled to make a second level oscillator (Poundstone, 1985: 89). Two shuttles and two blocks can be assembled to make a glider gun (Poundstone, 1985: 106). The glider gun generates gliders as output. We do not consider the output stream of gliders to be part of the gun. Many higher level machines are known (guns, rakes, puffer trains, breeders: see Poundstone, 1985: ch. 6). It is possible to assemble machines into logic gates (AND, OR, and NOT – see Poundstone, 1985: ch. 12). It is possible to make a self-reproducing machine that behaves like a simple living organism (Poundstone, 1985: ch. 12). Finally, it is possible to assemble simpler machines into a universal Turing machine (Rendell, 2002). Figure 6 shows a screen shot of Rendell’s Turing Machine.7
7. Persistence
There are two ways for a machine to end in the Game of Life. A machine comes to an extrinsic end iff its ability to run its program is disrupted by some external event. If a machine ends extrinsically, it does not end on its own. It is terminated by some accidental event in its environment. For instance, if a stray glider crashes into a blinker, both are destroyed. Both of those machines come to extrinsic ends. When a higher level machine comes to an extrinsic end, its own activity is no longer correlated with the coordinated activities of any set of lower level machines. It is no longer supported by a set of harmoniously interacting lower level machines. An extrinsic end is a hardware failure. We can apply the notion of an extrinsic end to any machine. Consider a digital electronic computer programmed to count to one million. If its CPU burns out at any count less than one million, then it has suffered a hardware failure. It has crashed.
A machine comes to an intrinsic end iff it reaches a fixed point. A fixed point is a shape that changes into itself. It is a still life. A fixed point is a halting state. For example, if we start an eater in state 1 (with a glider approaching from the northeast), then it will reach a fixed point in 4 steps. At that time, the operation of the eater ends intrinsically. Oscillators do not have fixed points. So they run forever. Mobile patterns like the glider do not have fixed points. So they run forever. For the sake of generality, the concept of an intrinsic end can be extended to cover machines that run forever. Their intrinsic ends are at infinity (the limit time ω). The notion of an intrinsic end can be applied to any machine. Consider a digital electronic computer programmed to count to one million. It ends intrinsically when and only when it reaches one million. It has fulfilled its nature. It halts.
A higher level machine is correlated with a plurality of lower level machines. On the one hand, this correlation is dependency. If it is dependency, then the activity of the higher level machine depends on the coordinated activities of the plurality of lower level machines. It is realized (supported, sustained) by those lower level machines. It supervenes on them. If their activities cease to generate shapes in the state-transition network of the higher level machine, it comes to an end. It ends extrinsically. If the correlation is dependency, then higher level machines are mere epiphenomena. They have no independent existence. It is natural to think of the correlation as dependency. When a glider smashes into a blinker on some life grid, they both degenerate into noise and disappear. The empirical evidence justifies the thesis that correlation is dependency. The empirical evidence justifies the thesis that every machine runs to its extrinsic end. It runs until it crashes.
On the other hand, the correlation is not dependency. The activity of the higher level machine is indeed coordinated with the activities of some plurality of lower level machines. It is entangled or harmonized with those activities. But it does not depend on them; it is not realized by them; it is not supported or sustained by them. It does not supervene on them. It is not an epiphenomenon. It is not a virtual object. Its existence is not less real. On the contrary, it has the same degree of being as the lower level machines over which it floats. It is an autonomous and independently existing entity. If a higher level machine is an independent entity, then it runs until it reaches an intrinsic end. It runs until it reaches the end specified in its own program (by its own rules, according to its own nature or essence). It does not run until it crashes; it runs until it halts.
Of course, a higher level machine is necessarily correlated with certain activities of lower level machines. If higher level machines are independent entities, then they generate the lower level machines with which they are correlated just as much as they are generated by those machines. How can this be? Suppose the glider crashes into the blinker. There is a life grid on which they are both destroyed. On this grid of destruction, the lowest level cells win and the glider and blinker lose. But if every higher level machine runs to its halting state, then the glider and blinker both generate life grids on which they continue running. The glider generates a life grid on which the blinker is not in its way (either because there is no blinker or the blinker is elsewhere). It generates a grid on which it wins. The blinker generates a life grid in which the glider will not hit it (either because there is no glider or the glider is elsewhere). It generates a grid on which it wins. If the glider and blinker generate these other life grids, then the life grid splits in at least 3 ways. It splits into history in which the cells win; into a history in which the glider wins; and into a history in which the blinker wins. It splits to form variant versions of itself. It thus splits into other possible life grids. Each cell in the life grid splits into a set of future counterparts. Some carry on according to the life rule (the cells win); others are adjusted so that they remain correlated with the higher level machines (the glider wins or the blinker wins).
Of course, one might object that lowest level machines cannot violate their own rules. For example, suppose time branches so that the blinker disappears. The glider continues on its merry way. But the disappearance of the blinker would be a miracle. The process that follows this branch is not a Game of Life (its cells aren’t running the life rule). A better alternative is that every higher level machine implies the actualization of every possible Game of Life in which it runs to its own intrinsic end. From the glider’s point of view, the blinker isn’t necessarily present. There are other games of life that resemble this one in every way except those that do not entail the existence of the blinker. So we can say that the glider implies the actualization of a plurality of games of life in which it runs to its intrinsic end. And the blinker implies the actualization of a plurality of games of life in which it runs to its intrinsic end. We thus have a tree not of time streams but of whole games of life.
A parity argument can be given for the thesis that correlation is not dependency (so that all higher level machines exist independently). Lower level and higher level machines are both just systems of if-then rules. The activity of the lower level machines is just the firing of these rules: truth flows from lower level antecedents to lower level consequents. Hence the lower level machines run to their intrinsic ends. But since the rules are of the same form in each case, what’s good for the lower level rules is equally good for the higher level rules. If truth flows through lower level rules, then it flows equally through higher level rules. If the lower level machines run to their intrinsic ends, then the higher level machines have the same right to run to their intrinsic ends. And we can neutralize the empirical objection: the evidence that one life grid exists is not evidence that others do not exist. So the evidence that the grid exists in which the glider and blinker collide is not evidence that the glider-friendly and blinker-friendly grids do not exist. The parity argument wins.
Accordingly, every software object runs to its intrinsic end. And what goes for the trivial Game of Life applies with the same logical force to software objects in our universe. Our reflections on the Game of Life are compatible with (and even support) similar reflections in quantum mechanics (QM). Specifically, our reflections support the Everett many-universes interpretation of QM (DeWitt, 1970; DeWitt & Graham, 1973; Deutsch, 1997; Rae, 2000: ch. 6). There are two interesting considerations here. The first is that the many-universes interpretation follows directly from the mathematical formalism of QM. It is a case in which the physics emerges from pure mathematics (DeWitt, 1970: 160 – 165). The second is that the many-universes interpretation is directly linked with quantum computation (Deutsch, 1985, 1997). Clearly, our thoughts about the existence of software are consistent with the notion that computation emerges from pure mathematics.
8. Applications
On this view, nature is stratified into a hierarchy of distinct levels. As Resnick puts it: “Interactions among objects at one level give rise to new types of objects at another level” (1994: 139). The bottom level in the Game of Life is the level of space-time points. Above that level, we find mobile patterns like gliders. These mobile patterns are like simple material particles. Particles are higher level machines. The next question is clear: how well do these ideas correspond to features of our actual universe?
A classical conception of material particles (like electrons and protons) is that they are tiny hard solid balls of stuff (call it matter). They are substances that stand to one another in spatial relations. They remain self-identical through changes. Hence they are enduring things (with time-indexed properties and relations). Field theories challenge this classical conception of particles in two ways. The first way is that field theories motivate substantivalism — space-time points are real physical things. The second way is that field theories treat particles as modifications of qualities of space-time points.
According to field theory, particles are not substances. A particle is something like a regular wrinkle in a carpet or like a vortex in a fluid (e.g. a tornado, hurricane, or whirlpool). We agree with field theorists that space-time points exist and carry the fundamental qualities of nature. We can think of these space-time points as little computers (like the lowest level machines in the Game of Life). Particles are regularities in the basic fields like the glider is a regularity in the Game of Life. Weinberg (1996) says:
For quite a long time many physicists thought that the world consisted of both fields and particles: the electron is a particle, described by a relativistically invariant version of the Schrodinger wave equation, and the electromagnetic field is a field, even though it also behaves like particles. ... In its mature form, the idea of quantum field theory is that quantum fields are the basic ingredients of the universe, and particles are just bundles of energy and momentum of the fields. In a relativistic theory the wave function is a functional of these fields, not a function of particle coordinates. Quantum field theory hence led to a more unified view of nature than the old dualistic interpretation in terms of both fields and particles.
Field theories are among our best scientific theories. So it’s entirely reasonable to think of space-time points as the lowest level machines in our universe. And elementary particles are higher level machines like gliders. And the hierarchy of higher level machines keeps rising – through atoms, molecules, and so on. The emergence of higher levels continues in biology. Kaufmann (1995: 24) portrays this idea nicely:
Life, in this view, is an emergent phenomenon arising as the molecular diversity of a prebiotic chemical system increases beyond a threshold of complexity. If true, then life is not located in the property of any single molecule — in the details — but is a collective property of systems of interacting molecules. Life, in this view, emerged whole and has always remained whole. Life, in this view, is not to be located in its parts, but in the collective emergent properties of the whole they create. Although life as an emergent phenomenon may be profound, its fundamental holism and emergence are not at all mysterious. A set of molecules either does or does not have the property that it is able to catalyze its own formation and reproduction from some simple food molecules. No vital force or extra substances is present in the emergent, self-reproducing whole. But the collective system does possess a stunning property not possessed by any of its parts. It is able to reproduce itself and to evolve. The collective system is alive. Its parts are just chemicals.
A swarm of flies or bees is a familiar example of a natural process in which a many interacting lower-level objects (the flies) produce a higher-level object (the swarm). It is easy to see the swarm of particles (flies) as a particle in its own right (at a higher level). Swarms of insects move like unified particles because they act in unison. The swarm is internally harmonized because all its members are coordinated relative to one another. The motion of all the insects is sufficiently coherent that a single entity, the swarm, emerges from and supervenes on their interactions. But just as a flock of birds is not a big bird, so a swarm of bugs is not a big bug. It is a distinct kind of higher-level object.
Bodies and brains are living systems. Continuing this reasoning from biology into psychology, we can argue that mental entities are software entities. Block (1995) says that the mind is the software of the brain. An early hypothesis identified neurons with logic gates (McCulloch & Pitts, 1943). Of course, that early hypothesis is false. Neurons are vastly more complicated than individual logic gates. But neurons are only finitely complex. So its entirely reasonable to identify a neuron with a vast network of logic gates. Since the brain is a network of neurons, it’s an even larger network of logic gates. Spike trains flowing through networks of neurons are like pulse trains flowing through networks of logic gates. If software objects are generated by the pulse trains in networks of logic gates, then they are generated by the spike trains over networks of neurons. If this is right, then mental entities like ideas are software entities over the brain. The mind itself might be the higher level machine (the software object) that the whole brain is running (or that the information processing circuitry of the whole body is running). Although this view says that the mind is not identical with the brain, it is not the old-fashioned Platonic or Cartesian dualism. The mind can’t exist without some brain on which it runs.
The idea of software machines has applications in physics, biology, and psychology. It is arguable that, in all those disciplines, collections of interacting lower-level objects generate higher-level objects with distinctive powers and properties. A glider in the Game of Life moves but its point-instants do not; a gas has properties of temperature and pressure but its molecules do not; a cell is alive but its molecules are not; a brain thinks but it's neurons do not; a species evolves but its individual organisms do not. The distinctive powers and properties of higher-level objects are real (Dennett, 1991). The motion of the glider is real; the temperature and pressure of a gas are real; the cognition of a brain is real; the evolution of a species is real. So long as mysticism is avoided, it’s fine to say that these higher level objects and properties are emergent (see Holland, 1998).
Finally, let’s return to where we started: most games of life are played on the semi-conductor (silicon) memories of electronic computers. These memories are smooth flat surfaces. They are life grids. A glider is a pattern of electrical charges running over some silicon surface. We argued that gliders are real entities. So if your computer runs a glider on some part of its memory, then there is a real higher level machine over that silicon surface. But the game of life is no different from any other program your computer might run. All software objects in your computer are patterns of electrical charge running over a silicon surface. These include all the data structures familiar from classical programming languages like C (e.g. chars, ints, arrays, structs, stacks, linked lists, and so on). They also include all the objects defined in object-oriented programming languages like C++ and Smalltalk. All these software objects are real and not merely epiphenomenal.
Notes
1 Sloman (1993) draws a platonic distinction between hardware and software objects. The software objects are non-physical abstract objects realized by or implemented by the concrete physical hardware objects. Sloman (1993: 74) says: “In a machine running text-processing software . . . there are letters, numerals, words, sentences, paragraphs, diagrams, chapters, etc., . . . However these textual entities are not physical entities and do not exist in the physical computer.” Sloman (1993: 78) says: “a word-processor manipulates words, paragraphs, etc., though these cannot be found in the underlying physical machine”. These claims are false. These “textual entities” are made of real mass-energy and are spatio-temporally located in the memory elements of the computer.2 Computers are not immaterial, abstract, or virtual objects. They are real concrete physical things. They do not manipulate symbols or process information. They are material engines that transform mass-energy patterns. MacLennan (1992: 638) defines computers as "programmable mass-energy manipulators":
We are accustomed to thinking of computers as abstract symbol-manipulating machines, realizations of universal Turing machines. I want to suggest that we think of computers as programmable mass-energy manipulators. The point is that the state of the computer is embodied in the distribution of real matter and energy, and that this matter and energy is redistributed under the control of the program. . . . the program defines the laws of nature that hold within the computer. Suppose a program defines laws that permit (real!) mass-energy structures to form, stabilize, reproduce, and evolve in the computer. If these structures satisfy the formal conditions of life, then they are real life, not simulated life, since they are composed of real matter and energy. Thus the computer may be a real niche for real artificial life — not carbon-based, but electron-based.
3 The program of a machine is determined by four rules. These rules define all the properties of the next future counterpart of a machine. Since machines don’t move, their x and y coordinates stay the same. These are: if (state = 0 and input is 3) then { x = x + 0; y = y + 0; state = 1 }; if (state = 0 and input is not 3) then { x = x + 0; y = y + 0; state = 0 }; if (state = 1 and input is 2 or 3) then { x = x + 0; y = y + 0; state = 1 }; if (state = 1 and input is neither 2 nor 3) then { x = x + 0; y = y + 0; state = 0 }.
4 We write the algorithm that generates the history of a blinker in a notation that resembles the computer programming language C:
Blinker(xStart, yStart, stateStart, n) {
x = xStart; y = yStart; // set initial center
state = stateStart; // set initial state
for i varying from 0 to n do {
rule-table { // fires only one rule
if (state = 0) then { x = x + 0; y = y + 0; state = 1;
write 000/111/000 centered on (x, y); }
if (state = 1) then { x = x + 0; y = y + 0; state = 0;
write 010/010/010 centered on (x, y); }}}}.
5 We write the algorithm that generates the history of a glider in a notation that resembles the computer programming language C:
Glider(xStart, yStart, stateStart) {
x = xStart; y = yStart; // set initial center;
state = stateStart; // set initial state
for i varying from 0 to n do {
rule-table { // fires only one rule
if (state = 0) then { x = x + 0; y = y + 0; state = 1;
write 010/001/111 centered on (x, y); }
if (state = 1) then { x = x + 0; y = y + 1; state = 2;
write 101/011/010 centered on (x, y); }
if (state = 2) then { x = x + 0; y = y + 0; state = 3;
write 001/101/011 centered on (x, y); }
if (state = 3) then { x = x + 1; y = y + 0; state = 0;
write 100/011/110 centered on (x, y); }}}}.
6 Our conception of software objects in terms of invariants has intriguing connections to the conception of material particles in terms of symmetry groups (see Castellani, 1998). The shapes are the members of the group. We cannot go into this in more detail here.
The screen shot is taken from LifeLab, a program that runs the Game of Life on Apple Computers. You can get LifeLab at 7 The screen shot is taken from LifeLab, a program that runs the Game of Life on Apple Computers. You can get LifeLab at http://www.trevorrow.com/lifelab. Accessed on 3 December 2007. The pattern was downloaded from Rendell’s website http://rendell-attic.org/gol/tm.htm. Accessed on 3 December 2007. References Adamatzky, A. (1998) "Universal dynamical computation in multidimensional
excitable lattices". International Journal of Theoretical Physics 37 (12), 3069 -
3108.
Castellani, E. (1998) "Galilean particles: An example of constitution of objects".
In E. Castellani (ed.) (1998) Interpreting Bodies: Classical and Quantum Objects
in Modern Physics. Princeton NJ: Princeton University Press, 181 – 194.
Chaitin, G. (1975) "Randomness and mathematical proof". Scientific American 232
(5), 47-52.
Colburn, T. (1999) "Software, abstraction, and ontology". The Monist 82 (1), 3 -
19.
Dennett, D. (1991) "Real patterns". Journal of Philosophy, 27-51.
Deutsch, D. (1985) "Quantum theory, the Church-Turing Principle and the universal
quantum computer". Proceedings of the Royal Society, Series A, 400, 97 - 117.
Deutsch, D. (1997) The Fabric of Reality. New York: Penguin.
In DeWitt, B., Graham, N. (1973) 155-166.
DeWitt, B., Graham, N. (1973) The Many-Worlds Interpretation of Quantum
Mechanics. Princeton, NJ: Princeton University Press.
Fredkin, E. (1991) "Digital mechanics: An informational process based on
reversible universal cellular automata". In Gutowitz, H. (1991) (ed.) Cellular
Automata: Theory and Experiment. Cambridge, MA: MIT Press, 254-270.
Fredkin, E., Landauer, R., Toffoli, T. (1982) (eds.) "Physics of computation".
(Conference Proceedings). International Journal of Theoretical Physics. Part I:
Vol. 21, Nos. 3 & 4 (April 1982); Part II: Vol. 21, Nos. 6 & 7 (June 1982); Part
III: Vol. 21, No. 12 (December 1982).
Hailperin, M., Kaiser, B., Knight, K. (1999) Concrete Abstractions: An
Introduction to Computer Science Using Scheme. Pacific Grove, CA: Brooks/Cole.
Holland, J. (1998) Emergence: From Chaos to Order. Reading, MA: Addison-Wesley.
Kaufmann, S. (1995) At Home in the Universe: The Search for the Laws of
Self-Organization and Complexity. New York: Oxford University Press.
MacLennan, B. (1992) "Synthetic ethology". In C. Langton, C. Taylor, J. Farmer,
S. Rasmussen, Artificial Life II. SFI Studies in the Sciences of Complexity,
Vol. 10. Reading, MA: Addison-Wesley, 631-659.
McCulloch, W. S., Pitts, W. H. (1943) "A logical calculus of the ideas immanent
in nervous activity". Bulletin of Mathematical Biophysics 5, 115-133.
Poundstone, W. (1985) The Recursive Universe: Cosmic Complexity and the Limits
of Scientific Knowledge. Chicago: Contemporary Books Inc.
Quine, W. V. O. (1969) Ontological Relativity and Other Essays. New York:
Columbia University Press.
Rae, A. (2000) Quantum Physics: Illusion or Reality? New York: Cambridge
University Press.
Rendell, P. (2002) "Turing universality of the Game of Life". In A. Adamatzky
(ed.) (2002), Collision-based Computation. New York: Springer, 513 - 539.
Resnick, M. (1994) Turtles, Termites, and Traffic Jams: Explorations in
Massively Parallel Microworlds. Cambridge, MA: MIT Press.
Sloman, A. (1993) "The mind as control system". In C. Hookway, D. Peterson
(eds.), Philosophy and Cognitive Science. Royal Institute of Philosophy
Supplement 34. New York: Cambridge University Press, 69 - 110.
Steinhart, E. (1998) "Digital metaphysics". In T. Bynum, J. Moor (eds.), The
Digital Phoenix. New York: Basil Blackwell, 117 - 134